题目内容
在平面直角坐标系中,O(0,0),P(6,8),将向量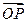 按逆时针旋转
按逆时针旋转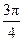 后,得向量
后,得向量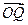 ,则点
,则点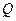 的坐标是( )
的坐标是( )
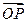 按逆时针旋转
按逆时针旋转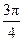 后,得向量
后,得向量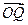 ,则点
,则点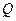 的坐标是( )
的坐标是( )A. |
B. |
C. |
D.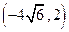 |
A
方法一:设 ,
,
则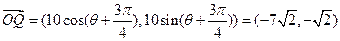 .
.
方法二:将向量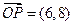 按逆时针旋转
按逆时针旋转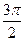 后得
后得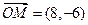 ,
,
设 =
=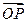 +
+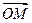 ,则
,则 =(14,2)
=(14,2)
因为|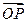 |=|
|=|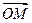 |,所以四边形OMQ′P为正方形,所以向量
|,所以四边形OMQ′P为正方形,所以向量 在正方形之对角线上。
在正方形之对角线上。
因为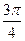 是
是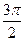 的一半,所以向量
的一半,所以向量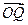 与
与 反向且|
反向且|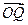 |=|
|=|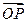 |=|
|=|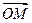 |=10
|=10
所以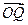 =-λ
=-λ (λ>0)
(λ>0)
由|-λ |=10得,λ=
|=10得,λ=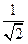 ,
,
所以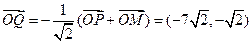 .
.
 ,
,则
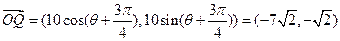 .
.方法二:将向量
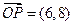 按逆时针旋转
按逆时针旋转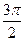 后得
后得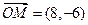 ,
,设
 =
=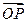 +
+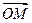 ,则
,则 =(14,2)
=(14,2)因为|
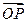 |=|
|=|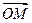 |,所以四边形OMQ′P为正方形,所以向量
|,所以四边形OMQ′P为正方形,所以向量 在正方形之对角线上。
在正方形之对角线上。因为
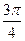 是
是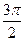 的一半,所以向量
的一半,所以向量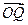 与
与 反向且|
反向且|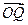 |=|
|=|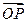 |=|
|=|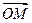 |=10
|=10所以
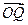 =-λ
=-λ (λ>0)
(λ>0)由|-λ
 |=10得,λ=
|=10得,λ=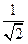 ,
,所以
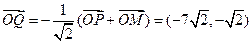 .
.
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
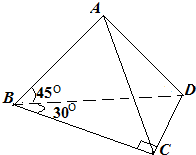
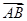 =
=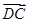 ,且
,且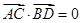 ,则四边形ABCD 是( )
,则四边形ABCD 是( )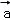 =(1,2),
=(1,2),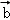 =(1,﹣1),则2
=(1,﹣1),则2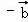 的夹角等于( )
的夹角等于( )
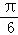
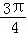
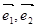 是两个单位向量,则下列结论中正确的是( )
是两个单位向量,则下列结论中正确的是( )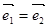
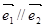
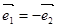
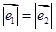
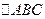 中,如果对任意实数
中,如果对任意实数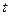 ,都有
,都有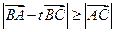 则
则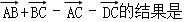 ( )
( )
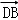


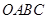 中,已知
中,已知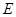 是线段
是线段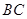 的中点,
的中点,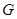 是
是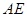 的中点,若
的中点,若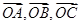 分别记为
分别记为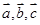 ,则用
,则用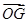 的结果为
的结果为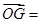 .
.