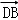题目内容
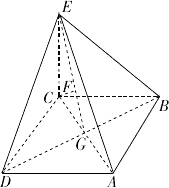
已知等腰梯形ABCD的上底AB=3,下底CD=1,高DO=1.以高线DO为折痕,将平面ADO折起,使得平面ADO⊥平面BCDO,点H为棱AC的中点.
(1)求直线OC与直线AB所成的余弦值;
(2)求平面ADO与平面ACB所成的锐二面角的余弦值;
(3)在平面ADO内找一点G,使得GH⊥平面ACB.

(1)求直线OC与直线AB所成的余弦值;
(2)求平面ADO与平面ACB所成的锐二面角的余弦值;
(3)在平面ADO内找一点G,使得GH⊥平面ACB.

(1)以O为原点,OD、OB、OA分别为x轴、y轴、z轴建立直角空间坐标系.
则C(1,1,0),A(0,0,1),B(0,2,0),H(
,
,
)…(3分)∴
=(1,1,0),
=(0,2,-1)∴cos<
,
>=
…(5分)
直线OC与直线AB所成的余弦值为
;
(2)设
=(x,y,z)是平面ACB的一个法向量,又
=(1,1,-1),
=(0,2,-1)
∴
不妨取y=1,则
=(1,1,2)…(7分)
又平面ADO的一个法向量为
=(0,2,0)
∴cos<
,
>=
,即为所求…(10分)
(3)设G(x,0,z),则
=(x-
,-
,z-
),…(12分)
要使GH⊥平面ACB,则
∥
,所以则G(0,0,-
)…(15分)
则C(1,1,0),A(0,0,1),B(0,2,0),H(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OC |
| AB |
| OC |
| AB |
| ||
| 5 |
直线OC与直线AB所成的余弦值为
| ||
| 5 |
(2)设
| n |
| AC |
| AB |
∴
|
| n |
又平面ADO的一个法向量为
| OB |
∴cos<
| n |
| OB |
| ||
| 6 |
(3)设G(x,0,z),则
| GH |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
要使GH⊥平面ACB,则
| GH |
| n |
| 1 |
| 2 |

练习册系列答案
相关题目


 与
与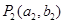 是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组
是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组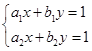 的解的情况是( )
的解的情况是( )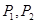 如何,总是无解
如何,总是无解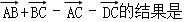 ( )
( )