题目内容
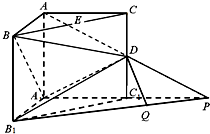
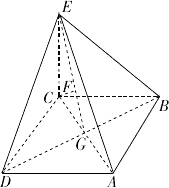
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.
(Ⅰ)求证:PB1∥平面A1BD;
(Ⅱ)求二面角A-A1D-B的大小;
(Ⅲ)在直线B1P上是否存在一点Q,使得DQ⊥平面A1BD,若存在,求出Q点坐标,若不存在请说明理由.
(Ⅰ)求证:PB1∥平面A1BD;
(Ⅱ)求二面角A-A1D-B的大小;
(Ⅲ)在直线B1P上是否存在一点Q,使得DQ⊥平面A1BD,若存在,求出Q点坐标,若不存在请说明理由.

以A1为原点,A1B、A1C、A1A分别为x轴、y轴、z轴,建立坐标系如图所示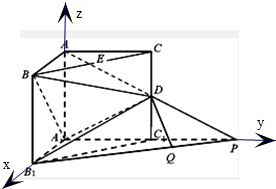
可得A1(0,0,0),B1(1,0,0),C1(0,1,0),
B(1,0,1),P(0,2,0)
(I)在△PAA1中,C1D=
AA1,则D(0,1,
)
∴
=(1,0,1),
=(0,1,
),
=(-1,2,0)
设平面BDA1的一个法向量为
=(x,y,z)
则
,取z=-1,得
=(1,
,-1)
∵
•
=1×(-1)+
×2+(-1)×0=0
∴直线PB1与平面BDA1的法向量垂直,可得PB1∥平面BDA1;
(II)由(I)知平面BDA1的一个法向量
=(1,
,-1)
又
=(1,0,0)为平面AA1D的一个法向量
∴cos<
,
>=
=
,即二面角A-A1D-B的平面角的余弦值为
因此,二面角A-A1D-B的大小为arccos
;
(III)根据点Q在B1P上,设Q的坐标为Q(λ,2-2λ,0)
∵D(0,1,
),∴
=(λ,1-2λ,-
)
若DQ⊥平面A1BD,则平面BDA1的法向量
=(1,
,-1)与
垂直
可得
•
=0,即λ×1+(1-2λ)×
+(-
)×(-1)=0,
解之得1=0矛盾
故向量
与
不可能垂直,即直线B1P上不存在一点Q,使得DQ⊥平面A1BD.

可得A1(0,0,0),B1(1,0,0),C1(0,1,0),
B(1,0,1),P(0,2,0)
(I)在△PAA1中,C1D=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| A1B |
| A1D |
| 1 |
| 2 |
| B1P |
设平面BDA1的一个法向量为
| a |
则
|
| a |
| 1 |
| 2 |
∵
| a |
| B1P |
| 1 |
| 2 |
∴直线PB1与平面BDA1的法向量垂直,可得PB1∥平面BDA1;
(II)由(I)知平面BDA1的一个法向量
| a |
| 1 |
| 2 |
又
| b |
∴cos<
| a |
| b |
| ||||
|
| 2 |
| 3 |
| 2 |
| 3 |
因此,二面角A-A1D-B的大小为arccos
| 2 |
| 3 |
(III)根据点Q在B1P上,设Q的坐标为Q(λ,2-2λ,0)
∵D(0,1,
| 1 |
| 2 |
| DQ |
| 1 |
| 2 |
若DQ⊥平面A1BD,则平面BDA1的法向量
| a |
| 1 |
| 2 |
| DQ |
可得
| a |
| DQ |
| 1 |
| 2 |
| 1 |
| 2 |
解之得1=0矛盾
故向量
| a |
| DQ |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与
与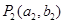 是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组
是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组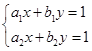 的解的情况是( )
的解的情况是( )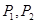 如何,总是无解
如何,总是无解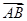 =
=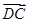 ,且
,且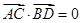 ,则四边形ABCD 是( )
,则四边形ABCD 是( )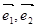 是两个单位向量,则下列结论中正确的是( )
是两个单位向量,则下列结论中正确的是( )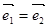
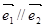
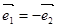
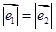
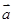 和
和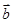 的夹角为1200,
的夹角为1200,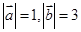 ,则
,则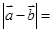 ( ).
( ).