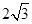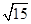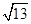题目内容
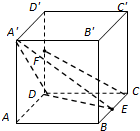
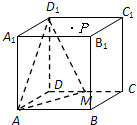
在边长为2的正方体ABCD-A′B′C′D′中,E是BC的中点,F是DD′的中点
(1)求证:CF∥平面A′DE
(2)求二面角E-A′D-A的平面角的余弦值.
(1)求证:CF∥平面A′DE
(2)求二面角E-A′D-A的平面角的余弦值.

证明(1):分别以DA,DC,DD'为x轴,y轴,z轴
建立空间直角坐标系,
则A'(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),…(2分)
则
=(2,0,2),
=(1,2,0),
设平面A'DE的法向量是
=(a,b,c),
则
,取
=(-2,1,2),…(4分)
=(0,-2,1),∵
•
=-2+2=0,∴
⊥
,
所以,CF∥平面A'DE.…(6分)
(2)由正方体的几何特征可得
=(0,2,0)是面AA'D的法向量
又由(1)中向量
=(-2,1,2)为平面A'DE的法向量
故二面角E-A'D-A的平面角θ满足;
cosθ=
=
即二面角E-A'D-A的平面角的余弦值为
…(8分)
建立空间直角坐标系,
则A'(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),…(2分)
则
| DA′ |
| DE |
设平面A'DE的法向量是
| n |
则
|
| n |
| CF |
| CF |
| n |
| CF |
| n |
所以,CF∥平面A'DE.…(6分)
(2)由正方体的几何特征可得
| DC |
又由(1)中向量
| n |
故二面角E-A'D-A的平面角θ满足;
cosθ=
| ||||
|
|
| 1 |
| 3 |
即二面角E-A'D-A的平面角的余弦值为
| 1 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
,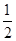 )
)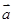 和
和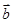 的夹角为1200,
的夹角为1200,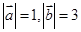 ,则
,则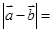 ( ).
( ).