题目内容
已知定义在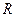 上的函数
上的函数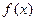 和数列
和数列 满足下列条件:
满足下列条件:
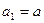 ,
,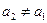 ,当
,当 且
且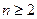 时,
时,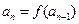 且
且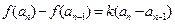 .
.
其中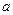 、
、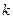 均为非零常数.
均为非零常数.
(1)若数列 是等差数列,求
是等差数列,求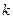 的值;
的值;
(2)令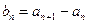
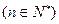 ,若
,若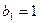 ,求数列
,求数列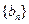 的通项公式;
的通项公式;
(3)试研究数列 为等比数列的条件,并证明你的结论.
为等比数列的条件,并证明你的结论.
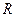 上的函数
上的函数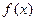 和数列
和数列 满足下列条件:
满足下列条件: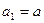 ,
,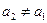 ,当
,当 且
且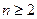 时,
时,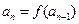 且
且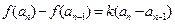 .
.其中
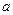 、
、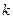 均为非零常数.
均为非零常数.(1)若数列
 是等差数列,求
是等差数列,求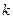 的值;
的值;(2)令
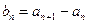
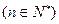 ,若
,若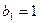 ,求数列
,求数列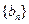 的通项公式;
的通项公式;(3)试研究数列
 为等比数列的条件,并证明你的结论.
为等比数列的条件,并证明你的结论.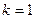 ,数列
,数列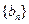 是一个公比为
是一个公比为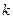 的等比数列,若
的等比数列,若

解:(1)由已知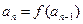 ,
,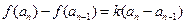
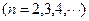 ,得
,得


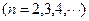
由数列 是等差数列,得
是等差数列,得

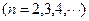
所以,
 ,
,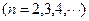 ,得
,得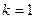 .………………………3分
.………………………3分
(2)由 ,可得
,可得
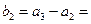
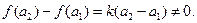
且当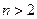 时,
时,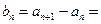
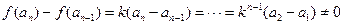
所以,当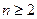 时,
时,
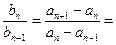
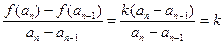 ,
,
因此,数列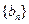 是一个公比为
是一个公比为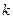 的等比数列.…………………………………………7分
的等比数列.…………………………………………7分
(3)解答一:写出必要条件,如,由(1)知,当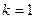 时,数列
时,数列 是等差数列,
是等差数列,
所以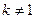 是数列
是数列 为等比数列的必要条件.
为等比数列的必要条件.
解答二:写出充分条件,如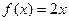 或
或 等,并证明
等,并证明
解答三: 是等比数列的充要条件是
是等比数列的充要条件是

充分性证明:
若
 ,则由已知
,则由已知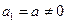 ,
,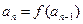
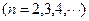 得
得
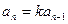
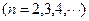
所以, 是等比数列.
是等比数列.
必要性证明:若 是等比数列,由(2)知,
是等比数列,由(2)知,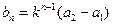
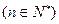
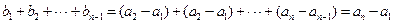
 ,
,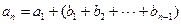 .
.
当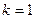 时,
时,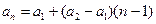
 .
.
上式对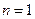 也成立,所以,数列
也成立,所以,数列 的通项公式为:
的通项公式为:
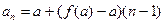
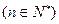 .
.
所以,当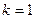 时,数列
时,数列 是以
是以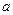 为首项,
为首项,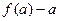 为公差的等差数列.
为公差的等差数列.
所以, .
.
当 时,
时,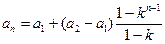
 .
.
上式对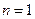 也成立,所以,
也成立,所以,
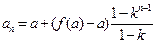
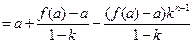
所以,
 .
.
即,等式 对于任意实数
对于任意实数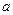 均成立.
均成立.
所以,
 .……………………………………………………………13分
.……………………………………………………………13分
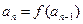 ,
,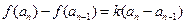
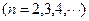 ,得
,得

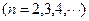
由数列
 是等差数列,得
是等差数列,得

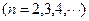
所以,

 ,
,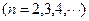 ,得
,得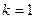 .………………………3分
.………………………3分(2)由
 ,可得
,可得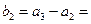
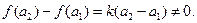
且当
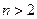 时,
时,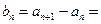
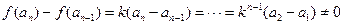
所以,当
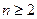 时,
时,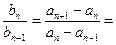
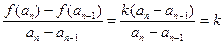 ,
,因此,数列
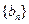 是一个公比为
是一个公比为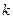 的等比数列.…………………………………………7分
的等比数列.…………………………………………7分(3)解答一:写出必要条件,如,由(1)知,当
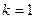 时,数列
时,数列 是等差数列,
是等差数列,所以
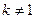 是数列
是数列 为等比数列的必要条件.
为等比数列的必要条件. 解答二:写出充分条件,如
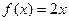 或
或 等,并证明
等,并证明 解答三:
 是等比数列的充要条件是
是等比数列的充要条件是

充分性证明:
若

 ,则由已知
,则由已知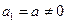 ,
,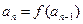
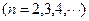 得
得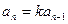
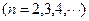
所以,
 是等比数列.
是等比数列.必要性证明:若
 是等比数列,由(2)知,
是等比数列,由(2)知,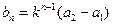
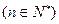
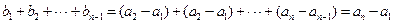
 ,
,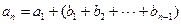 .
.当
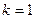 时,
时,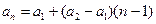
 .
.上式对
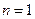 也成立,所以,数列
也成立,所以,数列 的通项公式为:
的通项公式为: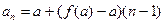
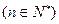 .
.所以,当
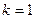 时,数列
时,数列 是以
是以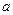 为首项,
为首项,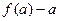 为公差的等差数列.
为公差的等差数列. 所以,
 .
.当
 时,
时,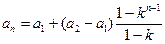
 .
. 上式对
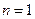 也成立,所以,
也成立,所以,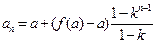
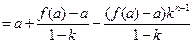
所以,

 .
.即,等式
 对于任意实数
对于任意实数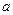 均成立.
均成立.所以,

 .……………………………………………………………13分
.……………………………………………………………13分
练习册系列答案
相关题目
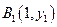 、
、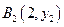 、…、
、…、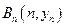 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数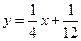 图像上的点,点列
图像上的点,点列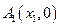 、
、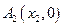 、…、
、…、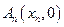 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中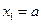 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点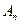 、
、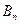 、
、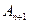 构成一个顶角的顶点为
构成一个顶角的顶点为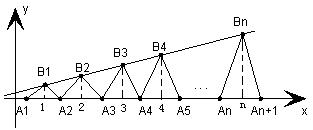
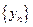 的通项公式,并证明
的通项公式,并证明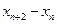 为常数,并求出数列
为常数,并求出数列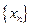 的通项公式;
的通项公式;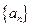 中,
中,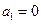 ,且对任意
,且对任意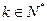 .
.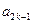 ,
,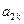 ,
,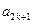 成等差数列,其公差为
成等差数列,其公差为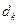 。
。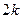 ,证明
,证明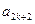 成等比数列(
成等比数列(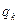 。 证明:对任意
。 证明:对任意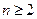 ,
,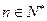 ,有
,有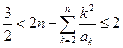
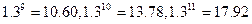 )
)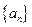 中,
中,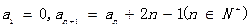 ,则数列
,则数列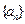 的首项
的首项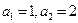 ,前
,前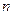 项和
项和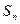 恒为正数,且当
恒为正数,且当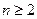 时,
时,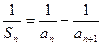 .
.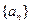 的通项公式;
的通项公式;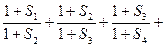
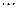
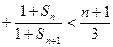 .
.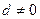 的等差数列{an}中的项组成一个新数列
的等差数列{an}中的项组成一个新数列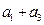 ,
, 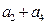 ,
,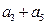 ,…,则下列说法正确的是
,…,则下列说法正确的是 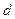 的等差数列
的等差数列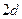 的等差数列
的等差数列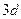 的等差数列
的等差数列