题目内容
在数列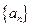 中,
中,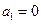 ,且对任意
,且对任意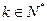 .
.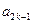 ,
,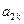 ,
,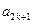 成等差数列,其公差为
成等差数列,其公差为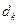 。
。
(Ⅰ)若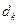 =
=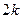 ,证明
,证明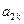 ,
,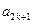 ,
,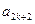 成等比数列(
成等比数列(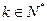 )
)
(Ⅱ)若对任意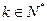 ,
,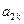 ,
,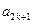 ,
,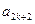 成等比数列,其公比为
成等比数列,其公比为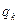 。 证明:对任意
。 证明:对任意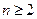 ,
,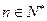 ,有
,有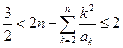
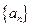 中,
中,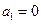 ,且对任意
,且对任意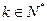 .
.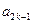 ,
,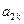 ,
,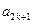 成等差数列,其公差为
成等差数列,其公差为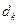 。
。(Ⅰ)若
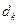 =
=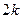 ,证明
,证明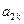 ,
,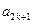 ,
,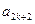 成等比数列(
成等比数列(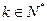 )
)(Ⅱ)若对任意
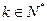 ,
,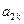 ,
,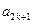 ,
,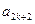 成等比数列,其公比为
成等比数列,其公比为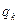 。 证明:对任意
。 证明:对任意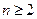 ,
,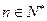 ,有
,有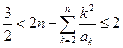
(Ⅰ)证明:由题设,可得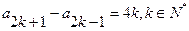 。
。
所以
=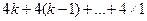
=2k(k+1)
由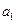 =0,得
=0,得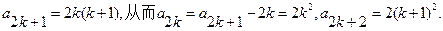
于是 。
。
所以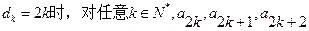 成等比数列。
成等比数列。
(Ⅱ)证法一:(i)证明:由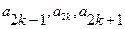 成等差数列,及
成等差数列,及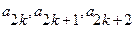 成等比数列,得
成等比数列,得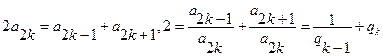
当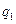 ≠1时,可知
≠1时,可知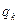 ≠1,k
≠1,k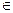
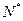
从而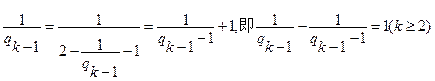
所以 是等差数列,公差为1。
是等差数列,公差为1。
(Ⅱ)证明: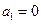 ,
,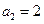 ,可得
,可得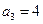 ,从而
,从而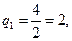
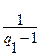 =1.由(Ⅰ)有
=1.由(Ⅰ)有
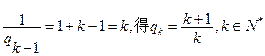
所以
因此,
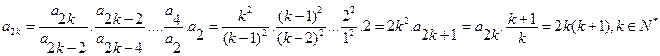 以下分两种情况进行讨论:
以下分两种情况进行讨论:
(1) 当n为偶数时,设n=2m(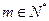 )
)
若m=1,则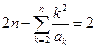 .
.
若m≥2,则
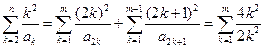 +
+
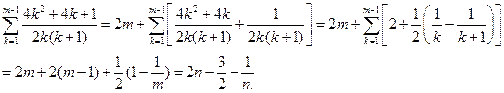
所以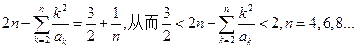
(2)当n为奇数时,设n=2m+1(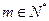 )
)
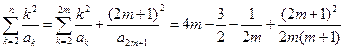
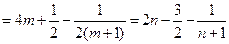
所以 从而
从而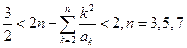 ···
···
综合(1)(2)可知,对任意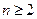 ,
,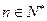 ,有
,有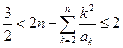
证法二:(i)证明:由题设,可得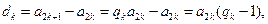
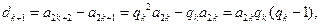 所以
所以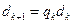
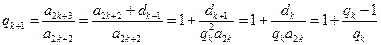
由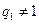 可知
可知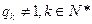 。可得
。可得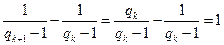 ,
,
所以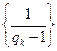 是等差数列,公差为1。
是等差数列,公差为1。
(ii)证明:因为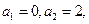 所以
所以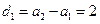 。
。
所以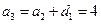 ,从而
,从而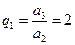 ,
,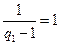 。于是,由(i)可知所以
。于是,由(i)可知所以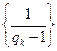 是公差为1的等差数列。由等差数列的通项公式可得
是公差为1的等差数列。由等差数列的通项公式可得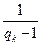 =
= 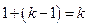 ,故
,故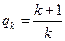 。
。
从而 。
。
所以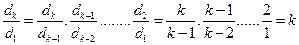 ,由
,由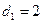 ,可得
,可得
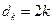 。
。
于是,由(i)可知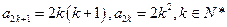
以下同证法一。
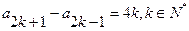 。
。所以

=
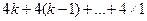
=2k(k+1)
由
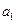 =0,得
=0,得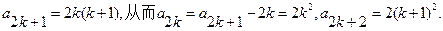
于是
 。
。所以
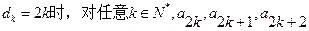 成等比数列。
成等比数列。(Ⅱ)证法一:(i)证明:由
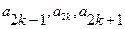 成等差数列,及
成等差数列,及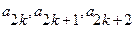 成等比数列,得
成等比数列,得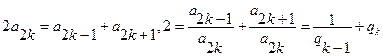
当
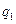 ≠1时,可知
≠1时,可知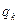 ≠1,k
≠1,k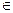
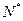
从而
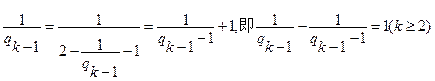
所以
 是等差数列,公差为1。
是等差数列,公差为1。(Ⅱ)证明:
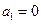 ,
,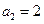 ,可得
,可得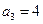 ,从而
,从而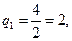
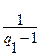 =1.由(Ⅰ)有
=1.由(Ⅰ)有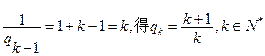
所以

因此,
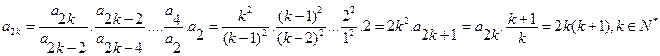 以下分两种情况进行讨论:
以下分两种情况进行讨论:(1) 当n为偶数时,设n=2m(
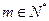 )
)若m=1,则
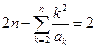 .
.若m≥2,则
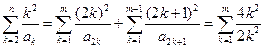 +
+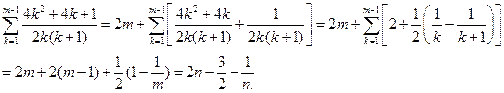
所以
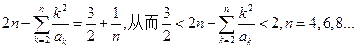
(2)当n为奇数时,设n=2m+1(
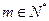 )
)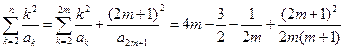
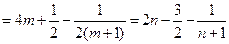
所以
 从而
从而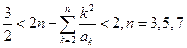 ···
···综合(1)(2)可知,对任意
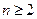 ,
,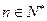 ,有
,有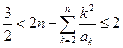
证法二:(i)证明:由题设,可得
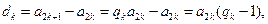
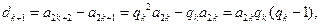 所以
所以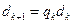
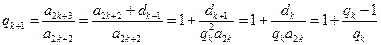
由
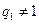 可知
可知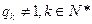 。可得
。可得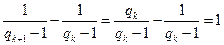 ,
,所以
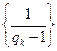 是等差数列,公差为1。
是等差数列,公差为1。(ii)证明:因为
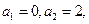 所以
所以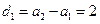 。
。所以
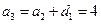 ,从而
,从而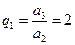 ,
,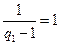 。于是,由(i)可知所以
。于是,由(i)可知所以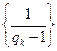 是公差为1的等差数列。由等差数列的通项公式可得
是公差为1的等差数列。由等差数列的通项公式可得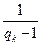 =
= 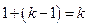 ,故
,故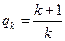 。
。从而
 。
。所以
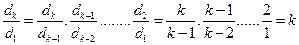 ,由
,由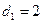 ,可得
,可得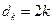 。
。于是,由(i)可知
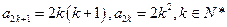
以下同证法一。

练习册系列答案
相关题目
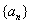 ,规定数列
,规定数列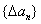 为数列
为数列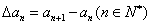 ;一般地,规定
;一般地,规定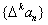 为
为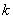 阶差分数列,其中
阶差分数列,其中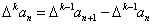 ,且
,且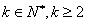 .
.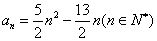 ,试证明
,试证明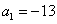 ,且满足
,且满足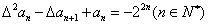 ,求数列
,求数列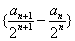 及
及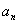 是否存在最小值,若存在求出其最小值,若不存在说明理由.
是否存在最小值,若存在求出其最小值,若不存在说明理由. 是首项为1公差为正的等差数列,数列
是首项为1公差为正的等差数列,数列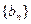 是首项为1的等比数列,设
是首项为1的等比数列,设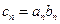
 ,且数列
,且数列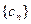 的前三项依次为1,4,12,
的前三项依次为1,4,12,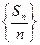 的前
的前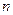 项的和Tn.
项的和Tn.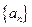 中,
中,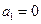 ,且对任意
,且对任意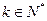 .
.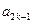 ,
,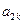 ,
,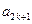 成等差数列,其公差为
成等差数列,其公差为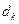 。
。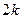 ,证明
,证明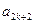 成等比数列(
成等比数列(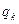 。
。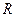 上的函数
上的函数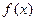 和数列
和数列 满足下列条件:
满足下列条件: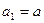 ,
,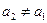 ,当
,当 且
且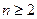 时,
时,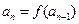 且
且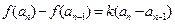 .
.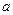 、
、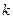 均为非零常数.
均为非零常数.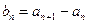
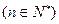 ,若
,若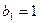 ,求数列
,求数列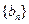 的通项公式;
的通项公式;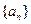 的前
的前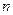 项和为
项和为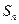 ,且点
,且点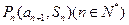 在函数
在函数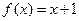 的图象上.
的图象上.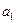 的值;
的值;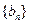 满足:
满足: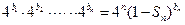 ,且
,且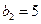 .求数列
.求数列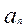 }的前n项和
}的前n项和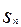 =
=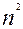 ,则
,则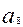 的值为
的值为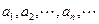 中的每一项都不为0。
中的每一项都不为0。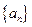 为等差数列的充分必要条件是:对任何
为等差数列的充分必要条件是:对任何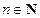 ,都有
,都有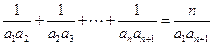 。
。