题目内容
【题目】已知椭圆![]() (
(![]() )的一个焦点是
)的一个焦点是![]() ,
, ![]() 为坐标原点,且椭圆短轴的两个三等分点与一个焦点构成正三角形,过点
为坐标原点,且椭圆短轴的两个三等分点与一个焦点构成正三角形,过点![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() ,当
,当![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:根据c=1,短轴的两个三等分点与一个焦点构成正三角形,得出a,b,写出椭圆的方程,设AB的方程,联立方程组,代入整理,利用 设而不求思想,借助根与系数关系解题,根据向量所提供的坐标关系结合根与系数关系,依据题目所给的向量差的模小于![]() ,解出
,解出![]() 的范围 。
的范围 。
试题解析:
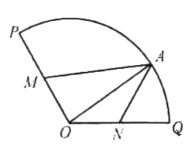
(Ⅰ)设![]() 为短轴的两个三等分点,因为△MNF为正三角形,
为短轴的两个三等分点,因为△MNF为正三角形,
所以![]() ,
, ![]() ,
, ![]() ,
,
因此,椭圆C的方程为![]() .
.
(Ⅱ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() 的方程为
的方程为![]() ,
,
由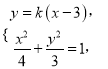 整理得
整理得![]() ,
,
由![]() ,得
,得![]()
![]()
![]() ,
,
则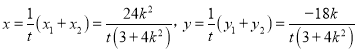 ,
,
由点![]() 在椭圆上,得
在椭圆上,得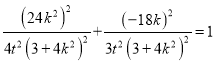 ,
,
化简得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,
,
即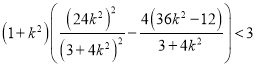 ,
,
即![]() ,所以
,所以![]() ,
,
即![]() ,因为
,因为![]() ,
,
所以![]() ,
,
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目