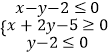题目内容
【题目】函数y=2x3﹣3x2﹣12x+5在区间[0，3]上最大值与最小值分别是（ ）
A.5，﹣15
B.5，﹣4
C.﹣4，﹣15
D.5，﹣16
【答案】A
【解析】解：由题意y'=6x2﹣6x﹣12 令y'＞0，解得x＞2或x＜﹣1
故函数y=2x3﹣3x2﹣12x+5在（0，2）减，在（2，3）上增
又y（0）=5，y（2）=﹣15，y（3）=﹣4
故函数y=2x3﹣3x2﹣12x+5在区间[0，3]上最大值与最小值分别是5，﹣15
故选A
【考点精析】认真审题，首先需要了解函数的最大(小)值与导数(求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值)．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
