题目内容
【题目】将一枚骰子投掷两次,所得向上点数分别为m和n,则函数y=mx2﹣nx+1在[1,+∞)上为增函数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:函数y=mx2﹣nx+1在[1,+∞)上为增函数, 等价于导数y′=2mx﹣n≥0在[1,+∞)上恒成立.
而x≥ ![]() 在[1,+∞)上恒成立即
在[1,+∞)上恒成立即 ![]() ≤1.
≤1.
∵将一骰子向上抛掷两次,所得点数分别为m和n的基本事件个数为36个,
而满足 ![]() ≤1包含的(m,n)基本事件个数为30个,不满足题意的点共有如图中6个点.
≤1包含的(m,n)基本事件个数为30个,不满足题意的点共有如图中6个点.
故函数y=mx2﹣nx+1在[1,+∞)上为增函数的概率是 ![]() =
= ![]() .
.
故选:D.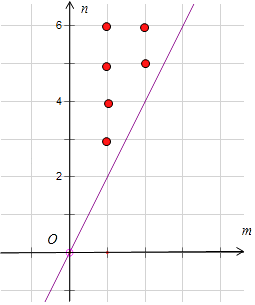
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如表:
API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为: S= 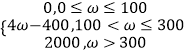 ,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关? 附:
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
k2= ![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |