题目内容
【题目】已知函数f(x)满足f(x+y)=f(x)+f(y),当x>0时,有![]() ,且f(1)=﹣2
,且f(1)=﹣2
(1)求f(0)及f(﹣1)的值;
(2)判断函数f(x)的单调性,并利用定义加以证明;
(3)求解不等式f(2x)﹣f(x2+3x)<4.
【答案】(1)0,2(2)减函数(3)(﹣2,1).
【解析】试题分析:(1)令x=y=0求f(0)=0;再令x=-y=1得f(0)=f(1)+f(-1);从而求解;(2)可判断函数f(x)是R上的减函数,利用定义证明;(3)由(2)知,f(2x)﹣f(x2+3x)<4可化为f(2x-x2-3x)<f(-2);从而得x2+x-2<0,从而解得
试题解析:(1)令x=y=0得,
f(0)=f(0)+f(0);
故f(0)=0;
令x=﹣y=1得,
f(0)=f(1)+f(﹣1);
故f(﹣1)=f(0)﹣f(1)=2; (3分)
(2)函数f(x)是R上的减函数,证明如下,
令x=﹣y得,f(0)=f(x)+f(﹣x);
故f(x)=﹣f(﹣x);
任取x1,x2∈R,且x1<x2,
则f(x1)﹣f(x2)=f(x1)+f(﹣x2)
=f(x1﹣x2)=﹣f(x2﹣x1),
故由f(x2﹣x1)<0知,﹣f(x2﹣x1)>0,
从而得f(x1)﹣f(x2)>0,
则函数f(x)是R上的减函数; (4分)
(3)由(2)知,
f(2x)﹣f(x2+3x)<4可化为
f(2x﹣x2﹣3x)<f(﹣2);
故x2+x﹣2<0,
解得,x∈(﹣2,1). (5分)

【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中![]() 所表示的数分别是多少?
所表示的数分别是多少?
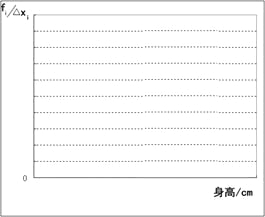
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?