题目内容
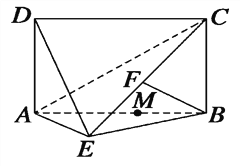
【题目】如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,
BF⊥平面ACE,且点F在CE上.
(1)求证:AE⊥BE;
(2)求三棱锥D—AEC的体积;
(3)设点M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,
使得MN∥平面DAE.
【答案】(1)![]() ;(2)
;(2)![]() .(3)点N为线段CE上靠近点C的一个三等分点
.(3)点N为线段CE上靠近点C的一个三等分点
【解析】试题分析:(1)先证明![]() ,可得AE⊥平面BCE,由此能证明
,可得AE⊥平面BCE,由此能证明![]() ;(2)由
;(2)由![]() ,能求出三棱锥
,能求出三棱锥![]() 的体积;(3)过点
的体积;(3)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,推导出
,推导出![]() 平面
平面![]() ,由此能求出当点
,由此能求出当点![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的一个三等分点时,
的一个三等分点时,![]() 平面
平面![]() .
.
试题解析:(1)证明 由AD⊥平面ABE及AD∥BC,
得BC⊥平面ABE,BC⊥AE,
而BF⊥平面ACE,所以BF⊥AE,
又BC∩BF=B,所以AE⊥平面BCE,
又BE平面BCE,故AE⊥BE.
在△ABE中,过点E作EH⊥AB于点H,
则EH⊥平面ACD.
由已知及(1)得EH=![]() AB=
AB=![]() ,S△ADC=2
,S△ADC=2![]() .
.
故VD—AEC=VE—ADC=![]() ×2
×2![]() ×
×![]() =
=![]() .(10分)
.(10分)
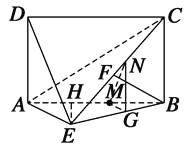
(3)解:在△ABE中,过点M作MG∥AE交BE于点G,在△BEC中过点G作GN∥BC交EC于点N,
连结MN,则由![]() =
=![]() =
=![]() =
=![]() ,得CN=
,得CN=![]() CE.
CE.
由MG∥AE,AE平面ADE,
MG平面ADE,则MG∥平面ADE.(12分)
再由GN∥BC,BC∥AD,AD平面ADE,GN平面ADE,
得GN∥平面ADE,所以平面MGN∥平面ADE.
又MN平面MGN,则MN∥平面ADE.(15分)
故当点N为线段CE上靠近点C的一个三等分点时,
MN∥平面ADE.
【方法点晴】本题主要考查线面平行的判定定理、直线和平面成的角的定义及求法、利用等积变换求三棱锥体积,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.

【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中![]() 所表示的数分别是多少?
所表示的数分别是多少?
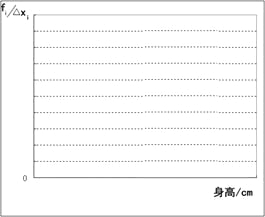
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?