Question

【题目】已知函数f（x）=x|x﹣2a|+a2﹣4a（a∈R）． （Ⅰ）当a=﹣1时，求f（x）在[﹣3，0]上的最大值和最小值；
（Ⅱ）若方程f（x）=0有3个不相等的实根x1 ， x2 ， x3 ， 求 + + 的取值范围．

Answer 1

【答案】解：（Ⅰ）∵a=﹣1，

∴f（x）=x|x+2|+5= ，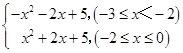

x∈[﹣2，0]时，4≤f（x）≤5，

x∈[﹣3，﹣2]时，2≤f（x）≤5，

∴f（x）min=f（﹣3）=2，f（x）max=f（0）=5；

（Ⅱ）∵f（x）= ，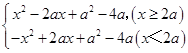

①若a＞0，∵方程f（x）=0有3个不相等的实根，

故x＜2a时，方程f（x）=﹣x2+2ax+a2﹣4a=0有2个不相等的实根，

x≥2a时，方程f（x）=x2﹣2ax+a2﹣4a=0有1个不相等的实根，

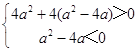∴ ，解得：2＜a＜4，

不妨设x1＜x2＜x3，则x1+x2=2a，x1x2=﹣a2+4a，x3=a+2 ，

∴ + + = + =﹣ ＞ ，

∴ + + 的范围是（ ，+∞），

②若a＜0，当x＞2a时，方程f（x）=x2﹣2ax+a2﹣4a=0的判别式小于0，

不符合题意；

③a=0时，显然不和题意，

故 + + 的范围是（ ，+∞）

【解析】（Ⅰ）求出f（x）的分段函数的解析式，从而求出函数的最大值和最小值即可；（Ⅱ）通过讨论a的范围，得到 + + 的表达式，从而求出a的范围即可．
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点，需要掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能正确解答此题．