题目内容
【题目】在平面直角坐标系
中，椭圆
的离心率为
，过椭圆右焦点
作两条互相垂直的弦
与
.当直线的斜率为0时，
.
（1）求椭圆的方程；
（2）试探究
是否为定值？若是，证明你的结论；若不是，请说明理由.
【答案】（1）
（2）
是定值；证明见解析
【解析】
（1）根据
，当直线
的斜率为0时，
.即
求解.
（2）分两种情况讨论，①当两条弦中一条弦所在直线的斜率为0时，另一条弦所在直线的斜率不存在，易得
.
②当两弦所在直线的斜率均存在且不为0时，设直线的方程为
，直线
的方程为
.将直线方程代入椭圆方程中并整理
，再利用弦长公式分别求解
即可.
（1）由题意知，当直线的斜率为0时，.
.
又
，
解得
，
，
所以椭圆方程为.
（2）①当两条弦中一条弦所在直线的斜率为0时，另一条弦所在直线的斜率不存在，
由题意知.
②当两弦所在直线的斜率均存在且不为0时，设直线的方程为，
，
，
则直线的方程为.
将直线方程代入椭圆方程中并整理得，
则
，
，
所以
.
同理，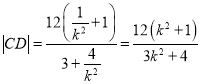
.
所以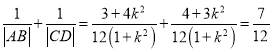
，
故是定值.
练习册系列答案
相关题目
【题目】某公司为了提高利润，从2012年至2018年每年对生产环节的改进进行投资，投资金额与年利润增长的数据如下表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利润增长 | 6.0 | 7.0 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
（1）请用最小二乘法求出
关于
的回归直线方程（结果保留两位小数）；
（2）现从2012—2018年这7年中抽出三年进行调查，记
年利润增长－投资金额，设这三年中
（万元）的年份数为
，求随机变量的分布列与期望.
参考公式：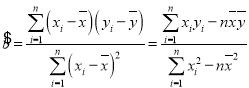
，
.
参考数据：
，
.
