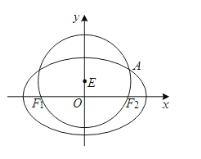
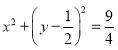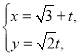题目内容
【题目】已知椭圆
的中心为坐标原点，焦点在
轴上，离心率
，以椭圆的长轴和短轴为对角线的四边形的周长为
.
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若经过点
的直线
交椭圆于
两点，是否存在直线
，使得到直线
的距离
满足
恒成立，若存在，请求出
的值；若不存在，请说明理由.
【答案】(Ⅰ)
；(Ⅱ)答案见解析.
【解析】分析：（Ⅰ）设椭圆
的标准方程为
，由题意可得
，
，
.则椭圆的标准方程为.
（Ⅱ）若直线
的斜率不存在,则直线
为任意直线都满足要求；当直线的斜率存在时，设其方程为：
，与椭圆方程联立有
，结合韦达定理可得
.则存在直线
，使得
到直线的距离
满足
恒成立.
详解：（Ⅰ）设椭圆的标准方程为，
∵
，∴
，又∵
，
∴
，由
，
解得，，.
所以椭圆的标准方程为.
（Ⅱ）若直线的斜率不存在,则直线为任意直线都满足要求；
当直线的斜率存在时，设其方程为：，
设
，
（不妨令
），
则
，
，
，
，
∵，∴
，解得
.
由
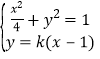得，
，
，.
综上可知存在直线，使得到直线的距离满足恒成立.
练习册系列答案
相关题目
