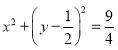题目内容
【题目】已知圆C的方程为:(x-3)2+(y-2)2=r2(r>0),若直线3x+y=3上存在一点P,在圆C上总存在不同的两点M,N,使得点M是线段PN的中点,则圆C的半径r的取值范围是________.
【答案】![]() .
.
【解析】
通过已知条件,求出点P的轨迹方程,而点P又在直线3x+y=3上,问题转化为直线与圆有公共点,即可求出r的取值范围.
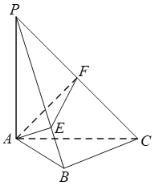
如图,连结PC,依次交圆于E,F两点,连结MF,EN,
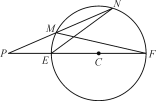
因为∠PNE和∠PFM都是弧![]() 的圆周角,由圆周角定理可得∠PNE=∠PFM,又∠NPE=∠FPM,所以△PNE∽△PFM,所以
的圆周角,由圆周角定理可得∠PNE=∠PFM,又∠NPE=∠FPM,所以△PNE∽△PFM,所以![]() ,即
,即![]() ,
,
而![]() ,
,
所以有![]() ,因为M是线段PN的中点,所以
,因为M是线段PN的中点,所以![]() ,
,
又因为M,N是圆上的任意两点,则有0<![]() ≤2r,即0<
≤2r,即0<![]() ≤8r2.
≤8r2.
设动点P(x,y),圆心C坐标为(3,2),则有0<(x-3)2+(y-2)2-r2≤8r2,即r2<(x-3)2+(y-2)2≤9r2,在一个圆环内,又因为P在直线3x+y=3上,所以直线3x+y=3与圆环有公共点,即直线与圆(x-3)2+(y-2)2=9r2有公共点,
则有![]() ,解得
,解得![]() ,所以圆C的半径r的取值范围是
,所以圆C的半径r的取值范围是![]() .
.
故答案为:![]()

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目