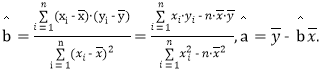题目内容
【题目】已知函数 ![]() .
.
(1)当m=1时,求证:对x∈[0,+∞)时,f(x)≥0;
(2)当m≤1时,讨论函数f(x)零点的个数.
【答案】
(1)证明:当m=1时, ![]() ,则f'(x)=ex﹣x﹣1,
,则f'(x)=ex﹣x﹣1,
令g(x)=ex﹣x﹣1,则g'(x)=ex﹣1,当x≥0时,ex﹣1≥0,即g'(x)≥0,
所以函数f'(x)=ex﹣x﹣1在[0,+∞)上为增函数,
即当x≥0时,f'(x)≥f'(0),所以当x≥0时,f'(x)≥0恒成立,
所以函数 ![]() ,在[0,+∞)上为增函数,又因为f(0)=0,
,在[0,+∞)上为增函数,又因为f(0)=0,
所以当m=1时,对x∈[0,+∞),f(x)≥0恒成立
(2)解:由(1)知,当x≤0时,ex﹣1≤0,所以g'(x)≤0,所以函数f'(x)=ex﹣x﹣1的减区间为(﹣∞,0],增区间为[0,+∞).所以f'(x)min=f'(0)=0,所以对x∈R,f'(x)≥0,即ex≥x+1.
①当x≥﹣1时,x+1≥0,又m≤1,∴m(x+1)≤x+1,∴ex﹣m(x+1)≥ex﹣(x+1)≥0,即f'(x)≥0,所以当x≥﹣1时,函数f(x)为增函数,又f(0)=0,所以当x>0时,f(x)>0,当﹣1≤x<0时,f(x)<0,所以函数f(x)在区间[﹣1,+∞)上有且仅有一个零点,且为0.
②当x<﹣1时,(ⅰ)当0≤m≤1时,﹣m(x+1)≥0,ex>0,所以f'(x)=ex﹣m(x+1)>0,
所以函数f(x)在(﹣∞,﹣1)上递增,所以f(x)<f(﹣1),且 ![]() ,
,
故0≤m≤1时,函数y=f(x)在区间(﹣∞,﹣1)上无零点.
(ⅱ)当m<0时,f'(x)=ex﹣mx﹣m,令h(x)=ex﹣mx﹣m,则h'(x)=ex﹣m>0,
所以函数f'(x)=ex﹣mx﹣m在(﹣∞,﹣1)上单调递增,f'(﹣1)=e﹣1>0,
当 ![]() 时,
时, ![]() ,又曲线f'(x)在区间
,又曲线f'(x)在区间 ![]() 上不间断,
上不间断,
所以x0∈ ![]() ,使f'(x0)=0,
,使f'(x0)=0,
故当x∈(x0,﹣1)时,0=f'(x0)<f'(x)<f'(﹣1)=e﹣1,
当x∈(﹣∞,x0)时,f'(x)<f'(x0)=0,
所以函数 ![]() 的减区间为(﹣∞,x0),增区间为(x0,﹣1),
的减区间为(﹣∞,x0),增区间为(x0,﹣1),
又 ![]() ,所以对x∈[x0,﹣1),f(x)<0,
,所以对x∈[x0,﹣1),f(x)<0,
又当 ![]() 时,
时, ![]() ,∴f(x)>0,
,∴f(x)>0,
又f(x0)<0,曲线 ![]() 在区间
在区间 ![]() 上不间断.
上不间断.
所以x1∈(﹣∞,x0),且唯一实数x1,使得f(x1)=0,
综上,当0≤m≤1时,函数y=f(x)有且仅有一个零点;当m<0时,函数y=f(x)有个两零点
【解析】(1)当m=1时, ![]() ,则f'(x)=ex﹣x﹣1,令g(x)=ex﹣x﹣1,利用导数研究其单调性极值与最值,可得函数f'(x)=ex﹣x﹣1在[0,+∞)上为增函数,即当x≥0时,f'(x)≥f'(0)=0,可得函数f(x)在(0,+∞)上为增函数,即可证明.(2)由(1)知,当x≤0时,ex﹣1≤0,所以g'(x)≤0,可得ex≥x+1.①当x≥﹣1时,x+1≥0,又m≤1,m(x+1)≤x+1,可得ex﹣m(x+1)≥0,即f'(x)≥0,可得:函数f(x)在区间[﹣1,+∞)上有且仅有一个零点,且为0.②当x<﹣1时,(ⅰ)当0≤m≤1时,﹣m(x+1)≥0,ex>0,可得f'(x)=ex﹣m(x+1)>0,函数f(x)在(﹣∞,﹣1)上递增,函数y=f(x)在区间(﹣∞,﹣1)上无零点. (ⅱ)当m<0时,f'(x)=ex﹣mx﹣m,令h(x)=ex﹣mx﹣m,则h'(x)>0,函数f'(x)=ex﹣mx﹣m在(﹣∞,﹣1)上单调递增,f'(﹣1)=e﹣1>0,可得函数存在两个零点.
,则f'(x)=ex﹣x﹣1,令g(x)=ex﹣x﹣1,利用导数研究其单调性极值与最值,可得函数f'(x)=ex﹣x﹣1在[0,+∞)上为增函数,即当x≥0时,f'(x)≥f'(0)=0,可得函数f(x)在(0,+∞)上为增函数,即可证明.(2)由(1)知,当x≤0时,ex﹣1≤0,所以g'(x)≤0,可得ex≥x+1.①当x≥﹣1时,x+1≥0,又m≤1,m(x+1)≤x+1,可得ex﹣m(x+1)≥0,即f'(x)≥0,可得:函数f(x)在区间[﹣1,+∞)上有且仅有一个零点,且为0.②当x<﹣1时,(ⅰ)当0≤m≤1时,﹣m(x+1)≥0,ex>0,可得f'(x)=ex﹣m(x+1)>0,函数f(x)在(﹣∞,﹣1)上递增,函数y=f(x)在区间(﹣∞,﹣1)上无零点. (ⅱ)当m<0时,f'(x)=ex﹣mx﹣m,令h(x)=ex﹣mx﹣m,则h'(x)>0,函数f'(x)=ex﹣mx﹣m在(﹣∞,﹣1)上单调递增,f'(﹣1)=e﹣1>0,可得函数存在两个零点.

 阅读快车系列答案
阅读快车系列答案【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查50人,并将调查情况进行整理后制成如表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,60) |
频数 | 10 | 10 | 10 | 10 | 10 |
赞成人数 | 3 | 5 | 6 | 7 | 9 |
(1)世界联合国卫生组织规定:[15,45)岁为青年,(45,60)为中年,根据以上统计数据填写以下2×2列联表:
青年人 | 中年人 | 合计 | |
不赞成 |
|
|
|
赞成 |
|
|
|
合计 |
|
|
|
(2)判断能否在犯错误的概率不超过0.05的前提下,认为赞成“车柄限行”与年龄有关? 附: ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
独立检验临界值表:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
(3)若从年龄[15,25),[25,35)的被调查中各随机选取1人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为ξ,求随机变量ξ的分布列和数学期望Eξ.
【题目】参与舒城中学数学选修课的同学对某公司的一种产品销量与价格进行了统计,得到如下数据和散点图.
定价x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

参考数据:
![]() ,
,
![]() .
.
(1)根据散点图判断y与x,z与x哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
(3)当定价为150元/千克时,试估计年销量.
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估计分别为