题目内容
【题目】已知动点P(x,y)与一定点F(1,0)的距离和它到一定直线l:x=4的距离之比为 ![]() .
.
(1)求动点P(x,y)的轨迹C的方程;
(2)己知直线l':x=my+1交轨迹C于A、B两点,过点A、B分别作直线l的垂线,垂足依次为点D、E.连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出定点的坐标,并给予证明;否则说明理由.
【答案】
(1)解:由题意得 ![]() =
= ![]() ,
,
即2 ![]() =丨x﹣4丨,
=丨x﹣4丨,
两边平方得:4x2﹣8x+4+4y2=x2﹣8x+16.整理得: ![]() .
.
∴动点P(x,y)的轨迹C的方程为椭圆 ![]()
(2)解:当m变化时,直线AE、BD相交于一定点N( ![]() ,0).
,0).
证明:如图,

当m=0时,联立直线x=1与椭圆 ![]() ,
,
得A(1, ![]() )、B(1,﹣
)、B(1,﹣ ![]() )、D(4,
)、D(4, ![]() )、E(4,﹣
)、E(4,﹣ ![]() ),
),
过A、B作直线x=4的垂线,得两垂足D(4, ![]() )、E(4,﹣
)、E(4,﹣ ![]() ),
),
由直线方程的两点式得:直线AE的方程为:2x+2y﹣5=0,直线BD的方程为:2x﹣2y﹣5=0,
方程联立解得x= ![]() ,y=0,
,y=0,
直线AE、BD相交于一点( ![]() ,0).
,0).
假设直线AE、BD相交于一定点N( ![]() ,0).
,0).
证明:设A(my1+1,y1),B(my2+1,y2),则D(4,y1),E(4,y2),
由 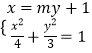 ,消去x,并整理得(3m2+4)y2+6my﹣9=0,
,消去x,并整理得(3m2+4)y2+6my﹣9=0,
△=36m2﹣4×(3m2+4)×(﹣9)=144m2+144>0>0,
由韦达定理得y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() .
.
由 ![]() =(my1﹣
=(my1﹣ ![]() ,y1),
,y1), ![]() =(
=( ![]() ,y2),
,y2),
则(my1﹣ ![]() )y2﹣
)y2﹣ ![]() y1=my1y2﹣
y1=my1y2﹣ ![]() (y1+y2)=m×(﹣
(y1+y2)=m×(﹣ ![]() )﹣
)﹣ ![]() ×(﹣
×(﹣ ![]() )=0
)=0
所以, ![]() ∥
∥ ![]() ,所以A、N、E三点共线,
,所以A、N、E三点共线,
同理可证B、N、D三点共线,所以直线AE、BD相交于一定点N( ![]() ,0)
,0)
【解析】(1)直接利用求轨迹方程的步骤,由题意列出满足动点P(x,y)到定点F(1,0)的距离和它到一定直线l:x=4的距离之比为 ![]() 的等式,整理后即可得到点P的轨迹;(2)如果存在满足条件的定点N,则该点对于m=0的直线也成立,所以先取m=0,与椭圆联立后解出A、B的坐标,同时求出D、E的坐标,由两点式写出AE、BD所在的直线方程,两直线联立求出N的坐标,然后证明该点对于m取其它值时也满足直线AE、BD是相交于定点N,方法是用共线向量基本定理.
的等式,整理后即可得到点P的轨迹;(2)如果存在满足条件的定点N,则该点对于m=0的直线也成立,所以先取m=0,与椭圆联立后解出A、B的坐标,同时求出D、E的坐标,由两点式写出AE、BD所在的直线方程,两直线联立求出N的坐标,然后证明该点对于m取其它值时也满足直线AE、BD是相交于定点N,方法是用共线向量基本定理.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】参与舒城中学数学选修课的同学对某公司的一种产品销量与价格进行了统计,得到如下数据和散点图.
定价x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

参考数据:
![]() ,
,
![]() .
.
(1)根据散点图判断y与x,z与x哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
(3)当定价为150元/千克时,试估计年销量.
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估计分别为