题目内容
19.如图在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,E为BC边中点.(1)求证:BD1∥平面C1DE;
(2)求三棱锥D1-DBC1的体积.
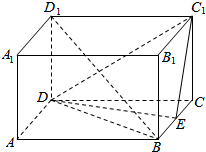
分析 (1)分别以DA、DC、DD1为x轴,y轴,z轴,建立空间直角坐标系,求出向量$\overrightarrow{B{D}_{1}}$和平面C1DE的法向量$\overrightarrow{n}$,利用向量法能证明BD1∥平面C1DE.
(2)由${V}_{{D}_{1}-DB{C}_{1}}={V}_{B-D{D}_{1}{C}_{1}}$,利用等体积法能求出三棱锥D1-DBC1的体积.
解答 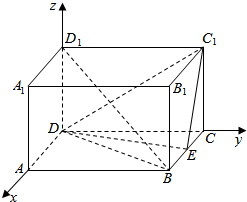 (1)证明:分别以DA、DC、DD1为x轴,y轴,z轴,建立空间直角坐标系,
(1)证明:分别以DA、DC、DD1为x轴,y轴,z轴,建立空间直角坐标系,
由已知得B(2,2,0),D1(0,0,1),D(0,0,0),C1(0,2,1),E(1,2,0),
∴$\overrightarrow{B{D}_{1}}$=(-2,-2,1),$\overrightarrow{DE}$=(1,2,0),$\overrightarrow{D{C}_{1}}$=(0,2,1),
设平面C1DE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{DE}•\overrightarrow{n}=x+2y=0}\\{\overrightarrow{D{C}_{1}}•\overrightarrow{n}=2y+z=0}\end{array}\right.$,取y=-1,得$\overrightarrow{n}$=(2,-1,2),
∴$\overrightarrow{B{D}_{1}}$$•\overrightarrow{n}$=-2×2+(-2)×(-1)+1×2=0,
∵BD不在平面C1DE内,
∴BD1∥平面C1DE.
(2)∵${S}_{△D{D}_{1}{C}_{1}}$=$\frac{1}{2}×D{D}_{1}×{D}_{1}{C}_{1}$=$\frac{1}{2}×1×2=1$,
点B到平面DD1C1的距离BC=2,
∴三棱锥D1-DBC1的体积:
${V}_{{D}_{1}-DB{C}_{1}}={V}_{B-D{D}_{1}{C}_{1}}$
=$\frac{1}{3}×{S}_{△D{D}_{1}{C}_{1}}×BC$
=$\frac{1}{3}×1×2$
=$\frac{2}{3}$.
点评 本题考查直线与平面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要注意向量法和等体积法的合理运用.
