题目内容
11.已知F1、F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左右焦点,P是椭圆上一点满足∠F1PF2=60°且|OP|=$\frac{\sqrt{3}}{2}$a,则椭圆离心率为$\frac{1}{2}$.分析 假设|F1P|=x,分别根据中线定理和余弦定理建立等式求得-c2+$\frac{5}{4}$a2=$\frac{4}{3}$(a2-c2),可得a和c的关系,即可求椭圆的离心率.
解答 解:不妨设|F1P|=x,则|F2P|=2a-x,
∵OP为三角形F1F2P的中线,∴根据三角形中线定理可知x2+(2a-x)2=$\frac{1}{2}$(4c2+3a2),
整理得x(2a-x)=-c2+$\frac{5}{4}$a2,
由余弦定理可知x2+(2a-x)2-x(2a-x)=4c2,
整理得x(2a-x)=$\frac{4}{3}$(a2-c2),
进而可知-c2+$\frac{5}{4}$a2=$\frac{4}{3}$(a2-c2),
∴a2=4c2
∴e=$\frac{c}{a}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了椭圆的定义、标准方程,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
3.下表所示关系为其函数图象上的若干点(x,y)满足的对应关系:
从这张表中可以看出这个函数的定义域为{1,2,3,4,5},值域为{54,55,56,57}.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 54 | 55 | 54 | 56 | 57 |
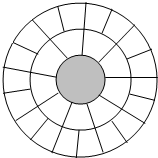 在我国古代,9是数学之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层的中心是一块天心石,围绕它的第1圈有9块石板,从第2圈开始,每1圈比前1圈多9块,共有9圈,则:
在我国古代,9是数学之极,代表尊贵之意,所以中国古代皇家建筑中包含许多与9相关的设计.例如,北京天坛圆丘的地面由扇环形的石板铺成(如图所示),最高一层的中心是一块天心石,围绕它的第1圈有9块石板,从第2圈开始,每1圈比前1圈多9块,共有9圈,则: