题目内容
4．函数f（x）=$\left\{\begin{array}{l}{lnx-{x}^{2}+2x（x＞0）}\\{{x}^{2}-2x-3（x≥0）}\end{array}\right.$的零点个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 分段函数的零点要讨论，对第一部分要作图．
解答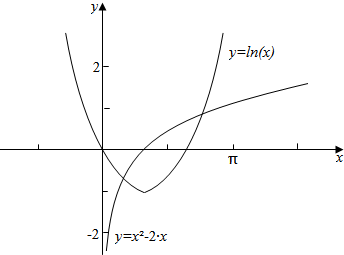 
解：①x≤0时，
f（x）=x2-2x-3=（x-1）2-4=0
解得，x=-1或x=3（舍去）．
②x＞0时，由y=lnx与y=x2-2x的图象可知，其有（0，+∞）上有两个交点，
故有两个解；
则函数f（x）=$\left\{\begin{array}{l}{lnx-{x}^{2}+2x（x＞0）}\\{{x}^{2}-2x-3（x≥0）}\end{array}\right.$的零点个数为3．
故选：D．
点评 本题考查了分段函数的零点个数，属于中档题．
练习册系列答案
相关题目
14．已知向量$\overrightarrow{a}$=（$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$）和$\overrightarrow{b}$=（-$\sqrt{3}$，1），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{6}$ | D． | $\frac{2π}{3}$ |
