题目内容
16.已知函数f(x)=x|x-4|(x∈R),若存在正实数k,使得方程f(x)=k在区间(2,+∞)上有两个根a,b,其中a<b,则ab-2(a+b)的取值范围是( )| A. | (2,2+2$\sqrt{2}$) | B. | (-4,0) | C. | (-2,2) | D. | (-4,2) |
分析 画出函数f(x)=x|x-4|=$\left\{\begin{array}{l}-{x}^{2}+4x,x<4\\{x}^{2}-4x,x≥4\end{array}\right.$的图象,数形结合分析出a+b的取值范围,再将ab-2(a+b)化为$\frac{{(a+b)}^{2}}{2}$-4(a+b),结合二次函数的图象和性质,可得答案.
解答 解:函数f(x)=x|x-4|=$\left\{\begin{array}{l}-{x}^{2}+4x,x<4\\{x}^{2}-4x,x≥4\end{array}\right.$的图象如下所示: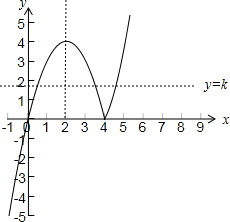
若存在正实数k,使得方程f(x)=k在区间(2,+∞)上有两个根a,b,其中a<b,
则a∈(2,4),b∈(4,2+2$\sqrt{2}$),a+b∈(4+2$\sqrt{2}$,8),
且-a2+4a=b2-4b,即4(a+b)=a2+b2,
则ab-2(a+b)=$\frac{(a+b)^{2}-({a}^{2}+{b}^{2})}{2}$-2(a+b)=$\frac{{(a+b)}^{2}}{2}$-4(a+b)∈(-4,0),
故选:B
点评 本题考查的知识点是分段函数的应用,二次函数的图象和性质,数形结合思想,难度中档.

练习册系列答案
相关题目
8.下列命题中,为真命题的是( )
| A. | 已知复数z=a+bi,a,b∈R,若|z|=b,则z是纯虚数 | |
| B. | 若复数a+bi(a,b∈R)是某方程的根,则a-bi也一定是此方程的根 | |
| C. | 两个共轭复数的差是纯虚数 | |
| D. | 复数集C和复平面内所有的点所组成的集合是一一对应的 |
5.若A={x|x∈N|x<2},可用列举法将集合{(x,y)|x∈A,y∈A}表示为( )
| A. | {(0,1)} | B. | {0,1} | C. | {(1,1),(1,2),(2,1),(2,2)} | D. | {(0,0),(0,1),(1,0),(1,1)} |