题目内容
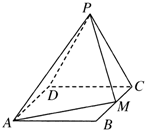
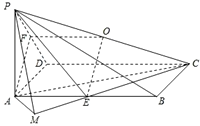
四棱锥P-ABCD的底面为菱形,且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=
,
E为PC的中点.
(1)求二面角E-AD-C的正切值;
(2)在线段PC上是否存在一点M,使PC⊥平面MBD成立?若存在,求出MC的长;若不存在,请说明理由.

| 6 |
E为PC的中点.
(1)求二面角E-AD-C的正切值;
(2)在线段PC上是否存在一点M,使PC⊥平面MBD成立?若存在,求出MC的长;若不存在,请说明理由.

(1)连AC、BD交于点O,连OE,则OE∥PA,从而OE⊥平面ABCD,
过点O作OF⊥AD于点F,连EF,则易证∠EFO就是所求二面角的平面角.
由ABCD是菱形,且∠ABC=120°,AB=1,得OF=
,
又OE=
PA=
,
∴在Rt△OEF中,有tan∠EFO=
=2
.(5分)
(2)证明:过点B作BM⊥PC于点M,连DM,
则∵△PBC≌△PDC,∴DM⊥PC,
∴PC⊥平面MBD,在△PBC中,PB=
,BC=1,PC=3,
∴cos∠PCB=
=
∴MC=BCcos∠PCB=
,
∴在PC上存在点M,且MC=
时,有PC⊥平面MBD.(10分)

过点O作OF⊥AD于点F,连EF,则易证∠EFO就是所求二面角的平面角.
由ABCD是菱形,且∠ABC=120°,AB=1,得OF=
| ||
| 4 |
又OE=
| 1 |
| 2 |
| ||
| 2 |
∴在Rt△OEF中,有tan∠EFO=
| OE |
| OF |
| 2 |
(2)证明:过点B作BM⊥PC于点M,连DM,
则∵△PBC≌△PDC,∴DM⊥PC,
∴PC⊥平面MBD,在△PBC中,PB=
| 7 |
∴cos∠PCB=
| 1+9-7 |
| 2•1•3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴在PC上存在点M,且MC=
| 1 |
| 2 |


练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目