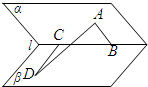
题目内容

平面α与平面β相交成一个锐二面角θ，平面α上的一个圆在平面β上的射影是一个离心率为
1
2
的椭圆，则θ等于（　　）
A．30°B．45°C．60°D．75°
由题意可得：平面α上的一个圆在平面β上的射影是一个离心率为
1
2
的椭圆，也可以说为：β上的一个离心率为
1
2
的椭圆在α上的射影是一个圆，
设圆的半径为r，所以b=r，
又因为
c
a
=
1
2
，并且b2=a2-c2，所以a=
2
3
3
r．
所以cosθ=
2r
2a
=
3
2
，所以θ=30°．
故选A．
练习册系列答案
相关题目
在直三棱柱ABC-A1B1C1中，AB=BC=CA=a，AA1=
2
a，求AB1与侧面AC1所成的角．
如图：在二面角α-l-β中，A、B∈α，C、D∈l，ABCD为矩形，p∈β，PA⊥α，且PA=AD，M、N依次是AB、PC的中点，
（1）求二面角α-l-β的大小
（2）求证：MN⊥AB
（3）求异面直线PA和MN所成角的大小．
四棱锥P-ABCD的底面为菱形，且∠ABC=120°，PA⊥底面ABCD，AB=1，PA=
6
，
E为PC的中点．
（1）求二面角E-AD-C的正切值；
（2）在线段PC上是否存在一点M，使PC⊥平面MBD成立？若存在，求出MC的长；若不存在，请说明理由．
在四棱锥P-ABCD中，侧面PDC是边长2的正三角形且与底面ABCD垂直，底面ABCD是面积为2
3
的菱形，∠ADC为锐角．
（1）求证：PA⊥CD
（2）求二面角P-AB-D的大小．
如图，在五面体P-ABCD中，底面ABCD是平行四边形，∠BAD=60°，AB=4，AD=2，PB=
15
，PD=
3
．
（1）求证：BD⊥平面PAD；
（2）若PD与底面ABCD成60°的角，试求二面角P-BC-A的大小．
已知点O在二面角α-AB-β的棱上，点P在α内，且∠POB=45°．若对于β内异于O的任意一点Q，都有∠POQ≥45°，则二面角α-AB-β的取值范围是______．
如图，直三棱柱ABC-A1B1C1的侧棱长为1，底面ABC为直角三角形，AB=AC=1，∠BAC=90°．则二面角B1-AC-B的大小为______；点A到平面BCC1B1的距离等于______．
如图，二面角α-l-β的棱l上有两点B、C，AB⊥l，CD⊥l，且AB⊆α，CD⊆β，若AB=CD=BC=2，AD=4，则此二面角的大小为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网