题目内容
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(I)根据![]()
![]() ,设直线方程为
,设直线方程为![]() ,
,![]()
确定![]() 的坐标,由
的坐标,由![]() 确定得到
确定得到![]() ,
,
再根据![]() 点在椭圆上,求得
点在椭圆上,求得![]() 进一步即得所求
进一步即得所求![]() ;
;
(2)由![]() 可设
可设![]() ,
,
得到椭圆的方程为![]() ,
,
由 得
得![]()
根据动直线![]() 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
得到![]() ,整理得
,整理得![]() .
.
确定![]() 的坐标
的坐标![]() ,
,
又![]() ,
, ![]()
![]()
若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,那么
,那么![]()
可得![]() ,由
,由![]() 恒成立,故
恒成立,故![]() ,得解.
,得解.
试题解析:(1)∵![]()
![]() ,设直线方程为
,设直线方程为![]() ,
,![]()
令![]() ,则
,则![]() ,∴
,∴![]() , 2分
, 2分
∴![]() 3分
3分
∵![]() ,∴
,∴![]() =
=![]() ,
,
整理得![]() 4分
4分
∵![]() 点在椭圆上,∴
点在椭圆上,∴![]() ,∴
,∴![]() 5分
5分
∴![]() 即
即![]() ,∴
,∴![]() 6分
6分
(2)∵![]() 可设
可设![]() ,
,
∴椭圆的方程为![]() 7分
7分
由 得
得![]() 8分
8分
∵动直线![]() 与椭圆有且只有一个公共点P
与椭圆有且只有一个公共点P
∴![]() ,即
,即![]()
整理得![]() 9分
9分
设![]()
![]() 则有
则有![]() ,
,![]()
∴![]() 10分
10分
又![]() ,
,![]()
![]()
若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,
,
∴![]() 恒成立
恒成立
整理得![]() , 12分
, 12分
∴![]() 恒成立,故
恒成立,故![]()
所求椭圆方程为![]() 13分
13分

 阅读快车系列答案
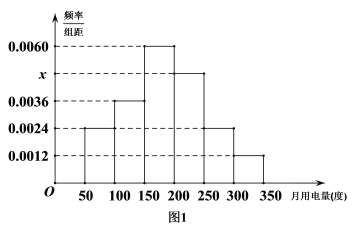
阅读快车系列答案【题目】从某小区抽取50户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图1.
A类用户 | B类用户 | |||||||
9 | 7 | 7 | 0 | 6 | ||||
8 | 6 | 5 | 1 | 7 | 8 | 9 | ||
9 | 8 | 2 | 8 | 5 | 6 | 7 | 8 | |
8 | 7 | 1 | 0 | 9 | 7 | 8 | 9 | |
图2
(1)求频率分布直方图中![]() 的值并估计这50户用户的平均用电量;(2)若将用电量在区间
的值并估计这50户用户的平均用电量;(2)若将用电量在区间![]() 内的用户记为
内的用户记为![]() 类用户,标记为低用电家庭,用电量在区间
类用户,标记为低用电家庭,用电量在区间![]() 内的用户记为
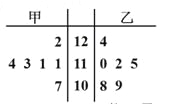
内的用户记为![]() 类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图2;若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有
类用户,标记为高用电家庭,现对这两类用户进行问卷调查,让其对供电服务进行打分,打分情况见茎叶图2;若打分超过85分视为满意,没超过85分视为不满意,请填写下面列联表,并根据列联表判断是否有![]() 的把握认为“满意度与用电量高低有关”?
的把握认为“满意度与用电量高低有关”?
满意 | 不满意 | 合计 | |
| |||
| |||
合计 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
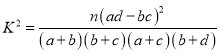 ,
,![]() .
.