题目内容
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 是圆
是圆![]() 的直径.若与圆
的直径.若与圆![]() 外离的圆
外离的圆![]() 上存在点
上存在点![]() ,连接
,连接![]() 与圆
与圆![]() 交于点
交于点![]() ,满足
,满足![]() ,则半径
,则半径![]() 的取值范围是_________.
的取值范围是_________.
【答案】![]() .
.
【解析】
推导出ON是△ABM的中位线,进而点M在以B为圆心,4为半径的圆周上,![]() ;点M可以认为是以O为圆心6为半径的圆上一点,这个圆记为
;点M可以认为是以O为圆心6为半径的圆上一点,这个圆记为![]() ,再由点M是在与圆O外离的圆
,再由点M是在与圆O外离的圆![]() 上的点,得到
上的点,得到![]() ,由此能求出存在符合题意的点M时,
,由此能求出存在符合题意的点M时,![]() 的取值范围.
的取值范围.
解:AM与圆O交于点N,![]() ,且圆心O是AB中点,
,且圆心O是AB中点,
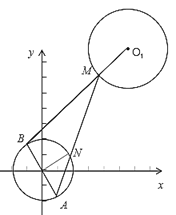
∴ON是△ABM的中位线,∴BM=2ON=4,
∴点M在以B为圆心,4为半径的圆周上,
∴![]() ;
;
又∵B是圆O上任意一点,
∴点M可以认为是以O为圆心6为半径的圆上一点,这个圆记为![]() ,
,
又∵点M是在与圆O外离的圆![]() 上的点,
上的点,
∴![]() ,
,
∴![]() .
.
∴存在符合题意的点M时,![]() 的取值范围是
的取值范围是![]() ,
,
故答案为:![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目