ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΨΑ«χ–όΫ®“ΜΕΑΗ¥Ι≈Ϋ®÷ΰΘ§Τδ¥ΑΜß…ηΦΤ»γΆΦΥυ Ψ.‘≤![]() ΒΡ‘≤–Ρ”κΨΊ–Έ
ΒΡ‘≤–Ρ”κΨΊ–Έ![]() Ε‘Ϋ«œΏΒΡΫΜΒψ÷ΊΚœΘ§«“‘≤”κΨΊ–Έ…œœ¬ΝΫ±Ώœύ«–Θ®
Ε‘Ϋ«œΏΒΡΫΜΒψ÷ΊΚœΘ§«“‘≤”κΨΊ–Έ…œœ¬ΝΫ±Ώœύ«–Θ®![]() ΈΣ…œ«–ΒψΘ©Θ§”κΉσ”“ΝΫ±ΏœύΫΜΘ®
ΈΣ…œ«–ΒψΘ©Θ§”κΉσ”“ΝΫ±ΏœύΫΜΘ®![]() Θ§
Θ§![]() ΈΣΤδ÷–ΝΫΗωΫΜΒψΘ©Θ§ΆΦ÷–“θ”Α≤ΩΖ÷ΈΣ≤ΜΆΗΙβ«χ”ρΘ§Τδ”ύ≤ΩΖ÷ΈΣΆΗΙβ«χ”ρ.“―÷Σ‘≤ΒΡΑκΨΕΈΣ1
ΈΣΤδ÷–ΝΫΗωΫΜΒψΘ©Θ§ΆΦ÷–“θ”Α≤ΩΖ÷ΈΣ≤ΜΆΗΙβ«χ”ρΘ§Τδ”ύ≤ΩΖ÷ΈΣΆΗΙβ«χ”ρ.“―÷Σ‘≤ΒΡΑκΨΕΈΣ1![]() Θ§«“
Θ§«“![]() Θ§…η
Θ§…η![]() Θ§ΆΗΙβ«χ”ρΒΡΟφΜΐΈΣ
Θ§ΆΗΙβ«χ”ρΒΡΟφΜΐΈΣ![]() .
.
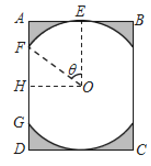
Θ®1Θ©«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωΕ®“ε”ρΘΜ
ΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωΕ®“ε”ρΘΜ
Θ®2Θ©ΗυΨί…ηΦΤ“Σ«σΘ§ΆΗΙβ«χ”ρ”κΨΊ–Έ¥ΑΟφΒΡΟφΜΐ±»÷Β‘Ϋ¥σ‘ΫΚΟ.Β±ΗΟ±»÷ΒΉν¥σ ±Θ§«σ±Ώ![]() ΒΡ≥ΛΕ».
ΒΡ≥ΛΕ».
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ ΫΈΣ
ΒΡΚ· ΐΙΊœΒ ΫΈΣ![]() Θ§Ε®“ε”ρΈΣ
Θ§Ε®“ε”ρΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΆΗΙβ«χ”ρ”κΨΊ–Έ¥ΑΟφΒΡΟφΜΐ±»÷ΒΉν¥σ ±Θ§![]() ΒΡ≥ΛΕ»ΈΣ1
ΒΡ≥ΛΕ»ΈΣ1![]() Θ°
Θ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
(1) ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ω…ΒΟ
Θ§Ω…ΒΟ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ ΫΈΣ
ΒΡΚ· ΐΙΊœΒ ΫΈΣ![]() Θ§Ε®“ε”ρΈΣ
Θ§Ε®“ε”ρΈΣ![]() ΘΜ
ΘΜ
(2)”…‘≠Κ· ΐ”κΒΦΚ· ΐΒΡΙΊœΒΩ…ΒΟΒ±![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷Β
”–Ήν¥σ÷Β![]() Θ§¥Υ ±
Θ§¥Υ ±![]()
‘ΧβΫβΈωΘΚ
Ϋβ:(1) ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
Υυ“‘![]() Θ§
Θ§
![]() Θ°
Θ°
Υυ“‘![]()
![]()
![]() Θ§
Θ§
“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§Υυ“‘Ε®“ε”ρΈΣ
Θ§Υυ“‘Ε®“ε”ρΈΣ![]() Θ°
Θ°
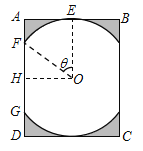
Θ®2Θ©ΨΊ–Έ¥ΑΟφΒΡΟφΜΐΈΣ![]() Θ°
Θ°
‘ρΆΗΙβ«χ”ρ”κΨΊ–Έ¥ΑΟφΒΡΟφΜΐ±»÷ΒΈΣ![]() Θ°
Θ°
…η![]() Θ§
Θ§![]() Θ°
Θ°
‘ρ![]()
![]()
![]()
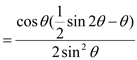 Θ§
Θ§
“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§Ι
Θ§Ι ![]() Θ§
Θ§
Υυ“‘Κ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒΞΒςΦθΘ°
…œΒΞΒςΦθΘ°
Υυ“‘Β±![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷Β
”–Ήν¥σ÷Β![]() Θ§¥Υ ±
Θ§¥Υ ±![]()
¥πΘΚΘ®1Θ©![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΙΊœΒ ΫΈΣ
ΒΡΚ· ΐΙΊœΒ ΫΈΣ![]() Θ§Ε®“ε”ρΈΣ
Θ§Ε®“ε”ρΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΆΗΙβ«χ”ρ”κΨΊ–Έ¥ΑΟφΒΡΟφΜΐ±»÷ΒΉν¥σ ±Θ§![]() ΒΡ≥ΛΕ»ΈΣ1
ΒΡ≥ΛΕ»ΈΣ1![]() Θ°
Θ°

 ΦΛΜνΥΦΈ§”≈Φ”ΩΈΧΟœΒΝ–¥πΑΗ
ΦΛΜνΥΦΈ§”≈Φ”ΩΈΧΟœΒΝ–¥πΑΗ ΜνΝΠ ‘ΨμœΒΝ–¥πΑΗ
ΜνΝΠ ‘ΨμœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ”–“Μ÷÷Οή¬κΘ§ΟςΈΡ «”…»ΐΗωΉ÷ΖϊΉι≥…Θ§Οή¬κ «”…ΟςΈΡΕ‘”ΠΒΡΈεΗω ΐΉ÷Ήι≥…Θ§±ύ¬κΙφ‘ρ»γœ¬±μΘΚΟςΈΡ”…±μ÷–ΟΩ“Μ≈≈»Γ“ΜΗωΉ÷ΖϊΉι≥…Θ§«“ΒΎ“Μ≈≈»ΓΒΡΉ÷ΖϊΖ≈‘ΎΒΎ“ΜΈΜΘ§ΒΎΕΰ≈≈»ΓΒΡΉ÷ΖϊΖ≈‘ΎΒΎΕΰΈΜΘ§ΒΎ»ΐ≈≈»ΓΒΡΉ÷ΖϊΖ≈‘ΎΒΎ»ΐΈΜΘ§Ε‘”ΠΒΡΟή¬κ”…ΟςΈΡΕ‘”ΠΒΡ ΐΉ÷Α¥œύΆ§ΒΡ¥Έ–ρ≈≈≥…“Μ≈≈Ήι≥….
| ΟςΈΡΉ÷Ζϊ | A | B | C | D |
Οή¬κΉ÷Ζϊ | 11 | 12 | 13 | 14 | |
| ΟςΈΡΉ÷Ζϊ | E | F | G | H |
Οή¬κΉ÷Ζϊ | 21 | 22 | 23 | 24 | |
| ΟςΈΡΉ÷Ζϊ | M | N | P | Q |
Οή¬κΉ÷Ζϊ | 1 | 2 | 3 | 4 |
…ηΥφΜζ±δΝΩ![]() ±μ ΨΟή¬κ÷–≤ΜΆ§ ΐΉ÷ΒΡΗω ΐΘ°
±μ ΨΟή¬κ÷–≤ΜΆ§ ΐΉ÷ΒΡΗω ΐΘ°
(Δώ)«σ![]() ΒΡΖ÷≤ΦΝ–ΚΆΥϋΒΡ ΐ―ßΤΎΆϊΘ°
ΒΡΖ÷≤ΦΝ–ΚΆΥϋΒΡ ΐ―ßΤΎΆϊΘ°