题目内容
【题目】已知椭圆C：
的离心率为
，椭圆C的四个顶点围成的四边形的面积为
．
求椭圆C的方程；
直线l与椭圆C交于
，
两个不同点，O为坐标原点，若
的面积为
，证明：
为定值．
【答案】（1）
（2）见解析
【解析】
由离心率为
，
，
，由
，解得：
，
，即可求得椭圆C的方程；
直线l的斜率不存在时，P，Q两点关于x轴对称，
，
，由三角形面积公式即可求得
和
的值，可得
的值，当直线斜率存在，设出直线方程
代入椭圆方程，利用
及韦达定理求得
和
的关系，利用点到直线的距离公式和弦长公式求得
的面积，求得m和k的关系式，即可证明为定值.
解：椭圆C：
的焦点在x轴上，离心率为，，
椭圆C的四个顶点围成的四边形的面积为
，即，
由，解得：，，
椭圆的标准方程为：；
证明：当直线
轴时，
，的面积
，
解得：
，
，
故
．
当直线l的斜率存在时，设直线l的方程为
，
，
联立
可得：
，
，即
，
由韦达定理可知
，
．
．
点O到直线l的距离为
则的面积
．
整理得：
，满足，代入
综上为定值.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】如图，在三棱台ABCDEF中，平面BCFE⊥平面ABC，∠ACB＝90°，BE＝EF＝FC＝1，BC＝2，AC＝3.
(1)求证：BF⊥平面ACFD；
(2)求二面角B-AD-F的平面角的余弦值．
【题目】近年来，我国电子商务蓬勃发展，有关部门推出了针对网购平台的商品和服务的评价系统，从该系统中随机选出100名交易者，并对其交易评价进行了统计，网购者对商品的满意率为0.6，对服务的满意率为0.75，其中对商品和服务都满意的有40人.
（1）根据已知条件完成下面的
列联表，并回答能否有
的把握认为“网购者对服务满意与对商品满意之间有关”？
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
（2）若对商品和服务都不满意者的集合为
.已知
中有2名男性，现从
中任取2人调查其意见.求取到的2人恰好是一男一女的概率.
附：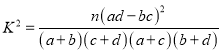 
(其中
为样本容量）
|
|
|
|
|
|
|
|
|
|
