题目内容
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1)椭圆的方程为![]() .
. ![]() ;(2)
;(2)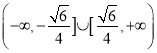
【解析】试题分析:(1)由椭圆方程可知![]() ,由已知
,由已知![]() 得
得![]() ,∴
,∴![]() ,平方得
,平方得![]() ,所以
,所以![]() ,又因为
,又因为![]() ,∴
,∴![]() ,解得
,解得![]() ,所以
,所以![]() ,因此
,因此![]() .所以,椭圆的方程为
.所以,椭圆的方程为![]() .
. ![]() . (2)因为直线
. (2)因为直线![]() 过点
过点![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,由点斜式得直线
,由点斜式得直线![]() 的方程为
的方程为![]() ,设
,设![]() ,把直线
,把直线![]() 的方程为
的方程为![]() 与椭圆方程联立消去
与椭圆方程联立消去![]() ,得
,得![]() ,因为2与点B的横坐标是此方程的两个根,用根于系数的关系得
,因为2与点B的横坐标是此方程的两个根,用根于系数的关系得![]() ,代入直线
,代入直线![]() 的方程从而得
的方程从而得![]() . 由
. 由![]() ,得
,得![]() ,设
,设![]() ,求两向量的坐标。由(1)知,
,求两向量的坐标。由(1)知, ![]() ,得向量坐标
,得向量坐标![]() ,
, 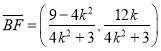 . 所以
. 所以![]() ,解得
,解得![]() .因为直线
.因为直线![]() 与直线
与直线![]() 垂直,所以直线
垂直,所以直线![]() 的斜率为
的斜率为![]() ,由直线的斜截式得直线
,由直线的斜截式得直线![]() 的方程为
的方程为![]() .联立直线
.联立直线![]() 的方程
的方程![]() 与直线
与直线![]() 的方程
的方程![]() ,设
,设![]() ,可解得点M的横坐标
,可解得点M的横坐标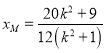 ,在
,在![]() 中,由大边对大角得
中,由大边对大角得![]() ,由两点间的距离公式得
,由两点间的距离公式得![]() ,化简得
,化简得![]() ,即
,即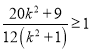 ,解不等式可得
,解不等式可得![]() ,或
,或![]() .
.
试题解析:解:(1)设![]() ,∵
,∵ ![]() ,∴
,∴ ![]() ,
, ![]()
又![]() ,∴
,∴ ![]() ,
, ![]() ,∴
,∴ ![]() ,
,
所以![]() ,因此
,因此![]() .
.
所以,椭圆的方程为![]() .
. ![]() .
.
(2)解:设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,
由方程组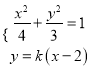 ,消去
,消去![]() ,得
,得![]() ,
,
解得![]() ,或
,或![]() ,由题意得
,由题意得![]() ,从而
,从而![]() .
.
由(1)知, ![]() ,设
,设![]() ,有
,有![]() ,
, 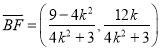 .
.
由![]() ,得
,得![]() ,所以
,所以![]() ,解得
,解得![]() .因此直线
.因此直线![]() 的方程为
的方程为![]() .
.
设![]() ,由方程组
,由方程组 ,消去
,消去![]() ,解得
,解得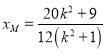 ,在
,在![]() 中,
中, ![]() ,即
,即![]() ,化简得
,化简得![]() ,即
,即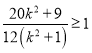 ,解得
,解得![]() ,或
,或![]() .
.
所以,直线![]() 的斜率的取值范围为
的斜率的取值范围为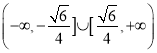 .
.

 名校课堂系列答案
名校课堂系列答案【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6 , 及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.