题目内容
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.

(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)由面面垂直性质定理得AC⊥平面BCFE,因此BF⊥AC.再根据平几知识得BF⊥FC.最后根据线面垂直判定定理得结论(2)过点F作FQ⊥AK于Q,由三垂线定理得BQ⊥AK.即∠BQF是二面角B-AD-F的平面角.再根据解三角形得二面角B-AD-F的平面角的余弦值
试题解析:(1)证明 延长AD,BE,CF相交于一点K,如图所示.
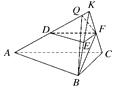
因为平面BCFE⊥平面ABC,平面BCFE∩平面ABC=BC,且AC⊥BC,
所以AC⊥平面BCFE,因此BF⊥AC.
又因为EF∥BC,BE=EF=FC=1,BC=2,所以△BCK为等边三角形,且F为CK的中点,则BF⊥CK,且CK∩AC=C,CK,AC都在平面ACFD内,
所以BF⊥平面ACFD.
(2)过点F作FQ⊥AK于Q,连接BQ.
因为BF⊥平面ACFD,AK在平面ACFD内,所以BF⊥AK,
则AK⊥平面BQF,BQ在平面BQF内,所以BQ⊥AK.
所以∠BQF是二面角B-AD-F的平面角.
在Rt△ACK中,AC=3,CK=2,得FQ=![]() .
.
在Rt△BQF中,FQ=![]() ,BF=
,BF=![]() ,得cos∠BQF=
,得cos∠BQF=![]() .
.
所以,二面角B-AD-F的平面角的余弦值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




