题目内容
【题目】已知直线l:y=kx+1(k≠0)与椭圆3x2+y2=a相交于A、B两个不同的点,记l与y轴的交点为C.
(Ⅰ)若k=1,且|AB|= ![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)若 ![]() =2
=2 ![]() ,求△AOB面积的最大值,及此时椭圆的方程.
,求△AOB面积的最大值,及此时椭圆的方程.
【答案】解:设A(x1,y1),B(x2,y2),
(Ⅰ)由 ![]() 得4x2+2x+1﹣a=0,
得4x2+2x+1﹣a=0,
则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
则|AB|= ![]() =
= ![]() ,解得a=2.
,解得a=2.
(Ⅱ)由 ![]() ,得(3+k2)x2+2kx+1﹣a=0,
,得(3+k2)x2+2kx+1﹣a=0,
则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
由 ![]() =2
=2 ![]() 得(﹣x1,1﹣y1)=2(x2,y2﹣1),
得(﹣x1,1﹣y1)=2(x2,y2﹣1),
解得x1=﹣2x2,代入上式得:
x1+x2=﹣x2=﹣ ![]() ,则x2=
,则x2= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
,
当且仅当k2=3时取等号,此时x2= ![]() ,x1x2=﹣2x22=﹣2×
,x1x2=﹣2x22=﹣2× ![]() ,
,
又x1x2= ![]() =
= ![]() ,
,
则 ![]() =﹣
=﹣ ![]() ,解得a=5.
,解得a=5.
所以,△AOB面积的最大值为 ![]() ,此时椭圆的方程为3x2+y2=5
,此时椭圆的方程为3x2+y2=5
【解析】(1)本小题的关键是线段AB长的表示,求得过程为![]() ;(2)本题关键在于三角形AOB面积的表示,求得过程为:S△AOB=
;(2)本题关键在于三角形AOB面积的表示,求得过程为:S△AOB=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某个体服装店经营某种服装,在某周内获得的纯利润y(单位:元)与该周每天销售这种服装的件数x之间的一组数据关系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求纯利润y与每天销售件数x之间的回归方程;
(2)若该周内某天销售服装20件,估计可获得纯利润多少元?
已知:![]() =280,
=280,![]() xiyi=3 487,
xiyi=3 487,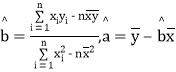 .
.
【题目】厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x/元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y/件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求线性回归方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =-20,
=-20, ![]() =
=![]() -
-![]()
![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)