题目内容
【题目】已知三点A(1,2),B(﹣3,0),C(3,﹣2).
(1)求证△ABC为等腰直角三角形;
(2)若直线3x﹣y=0上存在一点P,使得△PAC面积与△PAB面积相等,求点P的坐标.
【答案】
(1)证明:∵A(1,2),B(﹣3,0),C(3,﹣2).
∴AB=2 ![]() ,AC=2
,AC=2 ![]() ,BC=2
,BC=2 ![]() ,
,
即AB=AC,BC2=AB2+AC2,
即△ABC为等腰直角三角形
(2)解:直线AB的方程为: ![]() ,即x﹣2y+3=0,
,即x﹣2y+3=0,
直线AC的方程为: ![]() ,即2x+y﹣4=0,
,即2x+y﹣4=0,
∵P在直线3x﹣y=0上,故设P坐标为(a,3a),
∵AB=AC且△PAC面积与△PAB面积相等,
故P到直线AB和直线AC的距离相等,
即 ![]() =
= ![]() ,
,
即|5a﹣3|=|5a﹣4|,
解得:a= ![]() ,
,
故P点的坐标为:( ![]() ,
, ![]() )
)
【解析】(1)应用两点间距离公式可求三边长,再由勾股定理即可;
(2)由第(1)问可知AB=AC,那么两个三角形△PAC面积与△PAB面积相等,则点P到AB,AC的距离相等,应用点到直线的举例公式,即可;
【考点精析】掌握点到直线的距离公式是解答本题的根本,需要知道点![]() 到直线
到直线![]() 的距离为:
的距离为: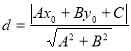 .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目


