Question

【题目】已知p：x2﹣2x﹣8≤0，q：x2+mx﹣6m2≤0，m＞0．
（1）若q是p的必要不充分条件，求m的取值范围；
（2）若p是q的充分不必要条件，求m的取值范围．

Answer 1

【答案】
（1）解：若命题p为真，则﹣2≤x≤4，

若命题q为真，则﹣3m≤x≤2m

若q是p的必要不充分条件，则 解得m≥2，

故m的取值范围为[2，+∞）

（2）解：若p是q的充分不必要条件，则q是p的充分不必要条件．

则 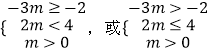解得 ，

故m的取值范围为

【解析】（1）首先解出不等式的解集，再根据q是p的必要不充分条件的定义，得到关于m的不等式组，解出即可。（2）根据逆否命题的真假与原命题的真假一致，得到p是q的充分不必要条件，则q是p的充分不必要条件，进而得到关于m的不等式组，解得即可。