题目内容
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:
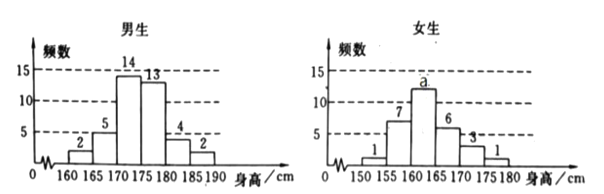
(1)估计该校男生的人数;并求出![]() 值
值
(2)估计该校学生身高在![]() 之间的概率;
之间的概率;
(3)从样本中身高在![]() 之间的女生中任选2人,求至少有1人身高在
之间的女生中任选2人,求至少有1人身高在![]() 之间的概率。
之间的概率。
【答案】(1)男生人数为400;![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据分层抽样总体及各层抽样比例相同求解;(2)用样本身高在![]() 之间的频数除以样本总数来估计;(3)列举所有情况,根据古典概型的概率公式求解.
之间的频数除以样本总数来估计;(3)列举所有情况,根据古典概型的概率公式求解.
解(1)样本中男生人数为40,由分层出样比例为10%估计全校男生人数为400。
由于以10%的比例抽取,所以样本中女生应该是30人,所以![]()
(2)由统计图知,样本中身高在![]() 之间的学生有
之间的学生有![]() 人,样本容量为70,
人,样本容量为70,
所以样本中学生身高在![]() 之间的频率
之间的频率![]() ,所以由
,所以由![]() 估计该校学身高在
估计该校学身高在![]() 之间的概率
之间的概率![]()
(3)样本中女生身高在![]() 之间的人数为4,身高在
之间的人数为4,身高在![]() 之间的人数为1。
之间的人数为1。
设![]() 表示事件“从样本中身高在
表示事件“从样本中身高在![]() 之间的女生中任选2人,至少有1人身高在
之间的女生中任选2人,至少有1人身高在![]() 之间”,通过列举可得
之间”,通过列举可得![]() 或者正面列举也是
或者正面列举也是![]() .
.

【题目】
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() .
.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】已知圆![]() 的圆心
的圆心![]() 的坐标为
的坐标为![]() ,且圆
,且圆![]() 与直线
与直线![]() :
:![]() 相切,过点
相切,过点![]() 的动直线
的动直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 的交点为
的交点为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)求![]() 的最小值;
的最小值;
(3)问:![]() 是否是定值?若是,求出这个定值;若不是,请说明理由.
是否是定值?若是,求出这个定值;若不是,请说明理由.
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了
两位选手,随机调查了![]() 个学生的评分,得到下面的茎叶图:
个学生的评分,得到下面的茎叶图:
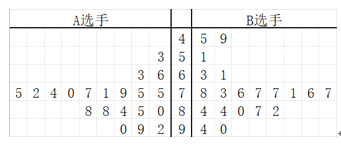
![]() 通过茎叶图比较
通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
![]() 校方将会根据评分记过对参赛选手进行三向分流:
校方将会根据评分记过对参赛选手进行三向分流:
所得分数 | 低于 |
| 不低于 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
记事件![]() “
“![]() 获得的分流等级高于
获得的分流等级高于![]() ”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件
”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件![]() 发生的概率.
发生的概率.
【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根据以上数据,绘制了散点图.
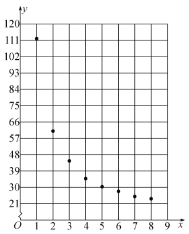
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() .
.
参考数据(其中![]() ):
):
|
|
|
|
|
|
|
|
183.4 | 0.34 | 0.115 | 1.53 | 360 | 22385.5 | 61.4 | 0.135 |
(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: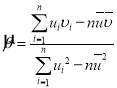 ,
,![]() ,相关系数
,相关系数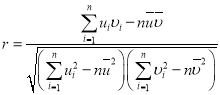 .
.