题目内容
17.在△ABC中,AB=4,AC=8,∠BAC=60°,延长CB到D,使BA=BD,当E点在线段AD上移动时,若$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则t=λ-μ的最大值是$\frac{{3+2\sqrt{3}}}{3}$.分析 根据条件判断三角形ABC是直角三角形,利用坐标法求出A,B,C,D的坐标,结合$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,即可找到λ和μ的关系,得到答案.
解答 解:∵AB=4,AC=8,∠BAC=60°,
∴三角形ABC是直角三角形,且BC=4$\sqrt{3}$,
∵BA=BD,∴BD=4,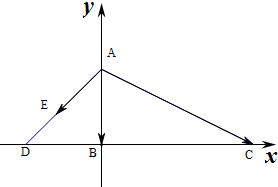
将三角形ABC放入直角坐标系中,
则D(-4,0),B(0,0),A(0,4),C(4$\sqrt{3}$,0),
则$\overrightarrow{AD}$=(-4,-4),$\overrightarrow{AB}$=(0,-4),$\overrightarrow{AC}$=(4$\sqrt{3}$,-4),
设E(x,y),则$\overrightarrow{AE}$=( )
设$\overrightarrow{AE}=t\overrightarrow{AD}$,t∈[0,1],
则$\overrightarrow{AE}=t\overrightarrow{AD}$=t(-4,-4)=(-4t,-4t),
∵$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$=λ(0,-4)+μ=(4$\sqrt{3}$,-4)=(4$\sqrt{3}$μ,-4λ-4μ),
∴$\left\{\begin{array}{l}{4\sqrt{3}μ=-4t}\\{-4λ-4μ=-4t}\end{array}\right.$,
即λ=$\frac{3+\sqrt{3}}{3}$t,μ=-$\frac{\sqrt{3}}{3}$t
∴λ-μ=$\frac{3+\sqrt{3}}{3}$t+$\frac{\sqrt{3}}{3}$t=$\frac{{3+2\sqrt{3}}}{3}$t,
∵t∈[0,1]
∴当t=1时,λ-μ取得最大值,最大值为$\frac{{3+2\sqrt{3}}}{3}$,
故答案为:$\frac{{3+2\sqrt{3}}}{3}$.
点评 本题主要考查平面向量的基本定理,即平面内任一向量都可由任意两不共线的向量唯一表示出来.建立坐标系,利用坐标法是解决本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | (-$\frac{π}{12}$,0) | B. | ($\frac{π}{12}$,0) | C. | (-$\frac{π}{6}$,0) | D. | ($\frac{π}{6}$,0) |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
| A. | 16(1-$\frac{1}{{2}^{n}}$) | B. | 16(1-$\frac{1}{{4}^{n}}$) | C. | $\frac{32}{3}$(1-$\frac{1}{{2}^{n}}$) | D. | $\frac{32}{3}$(1-$\frac{1}{{4}^{n}}$) |