题目内容
9．在区间（-1，1）内任取两个实数，则这两个实数的绝对值之和小于1的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
分析 本题可以利用几何概率模型求解，令两个数分别是x，y∈[-1，1]，所研究事件是“|x|+|y|＜1”，作出图形，由图形得出概率即得．
解答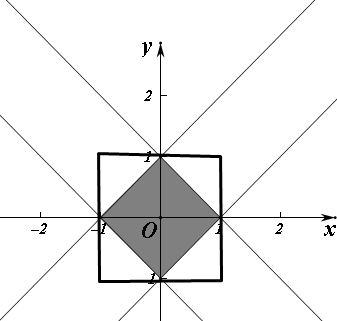 
解：设两个数分别是x，y；x，y∈[-1，1]，
所研究事件是“|x|+|y|＜1”
如图总的基本事件对应的面积是4，
事件“|x|+|y|＜1”对应的面积是大正方形面积的一半，
则它们的绝对值之和大于1的概率是：$\frac{1}{2}$．
故选：A．
点评 本题考查了几何概型的概率求法，关键是画出图形，利用面积比求概率．
练习册系列答案
名校课堂系列答案
相关题目
11．不等式x2-2x-3＞0的解集为（ ）
| A． | （-3，1） | B． | （-∞，-3）∪（1，+∞） | C． | （-1，3） | D． | （-∞，-1）∪（3，+∞） |
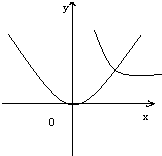已知曲线y=$\frac{1}{x}$和y=x2它们交于点P，过P点的两条切线与x轴分别交于A，B两点．求△ABP的面积．
1．已知集合A={x|x2-x≤0}，B={x|-2≤x≤0}，则A∩∁RB=（ ）
| A． | ∅ | B． | {x∈R|x≠0} | C． | {x|0＜x≤1} | D． | R |