题目内容
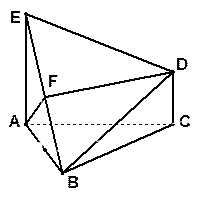
如图，已知△ABC是正三角形，EA、CD都垂直于平面ABC，且EA=AB=2DC,F是BE的中点，求证：(1) FD∥平面ABC; (2)FD⊥平面ABE; (3) AF⊥平面EDB.
(1) 见解析
(2) 见解析
(3)见解析
(2) 见解析
(3)见解析
(1)取AB中点G,连结CG,FG.因为F是中点,所以
FG=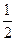
EA, FG∥EA.又CD=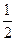EA,CD∥EA.所以四边形CDFG为平行四边形,FD∥CG,所以FD∥平面ABC.--------------------------5分
(2)
△ABC是正三角形,G是中点,
CG⊥AB,-----------------------7分
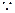EA⊥平面ABC,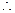EA⊥CG,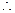CG⊥平面EAB. --------------------------9分
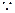FD∥CG,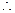FD⊥平面ABE.--------------------------10分
(3)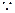FD⊥平面ABE,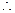FD⊥AF,--------------------------12分
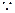EA=AB,F是中点,AF⊥EB,--------------------------14分
AF⊥平面EDB.--------------------------16分
FG=
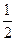EA, FG∥EA.又CD=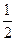EA,CD∥EA.所以四边形CDFG为平行四边形,FD∥CG,所以FD∥平面ABC.--------------------------5分(2)
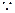△ABC是正三角形,G是中点,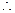CG⊥AB,-----------------------7分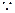EA⊥平面ABC,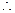EA⊥CG,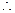CG⊥平面EAB. --------------------------9分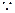FD∥CG,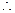FD⊥平面ABE.--------------------------10分(3)
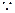FD⊥平面ABE,FD⊥AF,--------------------------12分EA=AB,F是中点,AF⊥EB,--------------------------14分AF⊥平面EDB.--------------------------16分
练习册系列答案
应用题作业本系列答案
相关题目
BD = O，A1C1
B1D1 = O1，E是O1A的中点．
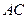⊥BD垂足为H,PH是四棱锥的高，E为AD中点.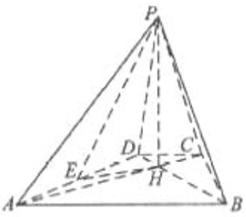 
=
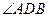=60°，求直线PA与平面PEH所成角的正弦值.
B
=AB，D为BB
的中点，E为AB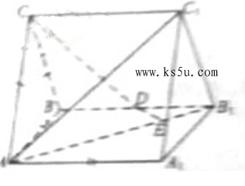
与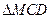
都是边长为2的正三角形，
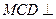平面
，
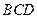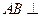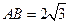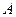平面
.
到平面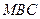
的距离；
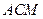与平面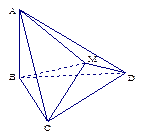
圈上有甲、已两地，甲地位于东径
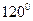，乙地位于西径
，则地球（半径为R）表面上甲、乙两地的最短距离为_________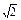 
a，则它的5个面中，互相垂直的面有 对.
，
，
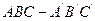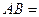
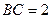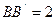，N、M分别是
、
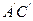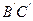的中点
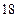
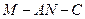的余弦值
