题目内容
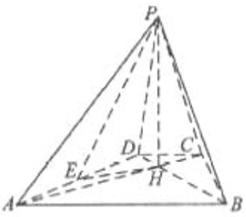
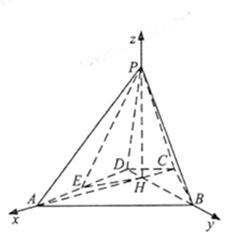
如图,己知四棱锥P-ABCD的底面为等腰梯形,AB∥CD, ⊥BD垂足为H,PH是四棱锥的高,E为AD中点.
⊥BD垂足为H,PH是四棱锥的高,E为AD中点.
(Ⅰ)证明:PE⊥BC
(Ⅱ)若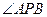 =
=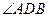 =60°,求直线PA与平面PEH所成角的正弦值.
=60°,求直线PA与平面PEH所成角的正弦值.
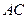 ⊥BD垂足为H,PH是四棱锥的高,E为AD中点.
⊥BD垂足为H,PH是四棱锥的高,E为AD中点. 
(Ⅰ)证明:PE⊥BC
(Ⅱ)若
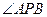 =
=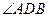 =60°,求直线PA与平面PEH所成角的正弦值.
=60°,求直线PA与平面PEH所成角的正弦值.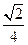
解:
(I)以
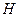 为原点,
为原点,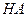 ,
,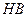 ,
,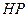 分别为
分别为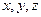 轴,线段
轴,线段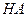 的长为单位长度,建立坐标系如图所示。
的长为单位长度,建立坐标系如图所示。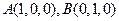
设
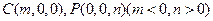
则
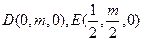
可得
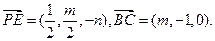
∵

∴

(II)由已知条件可得
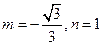 ,则
,则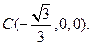
∴
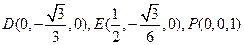
设
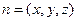 是平面
是平面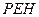 的法向量
的法向量则
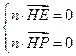
∴
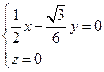
因此可以取
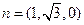
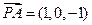
可得
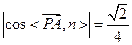
∴直线
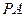 和平面
和平面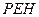 所成角的正弦值为
所成角的正弦值为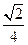

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
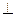 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD
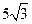 cm
cm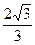 cm
cm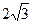 cm
cm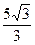 cm
cm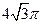 的球面上有
的球面上有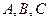 三点,
三点,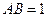 ,
,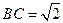 ,
,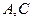 两点的球面距离为
两点的球面距离为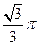 ,则球心到平面
,则球心到平面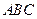 的距离为_______________.
的距离为_______________. 平面ABCD,M、N分别是AB、PC的中点
平面ABCD,M、N分别是AB、PC的中点 PDA=
PDA= 求证:MN
求证:MN 
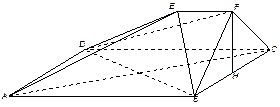
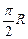 ,则过A、B的平面中,与球心的最大距离是
,则过A、B的平面中,与球心的最大距离是 
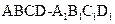 中,
中, ,AB=2,点E在棱AB上移动.
,AB=2,点E在棱AB上移动.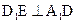 ;
;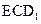 的距离;
的距离;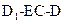 的大小为
的大小为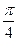 .
.