题目内容
2.已知数列{an}中,a1=1,且对于任意的n∈N*,a4n+1,a4n+2,a4n+3构成公差为2的等差数列,而a4n+3,a4n+4,a4n+5构成公比为$\frac{1}{2}$的等比数列,且an<M恒成立,则M的最小值为$\frac{16}{3}$.分析 可由题意求得数列的前15项,观察得到,连续5项,a4n+1,a4n+2,a4n+3,a4n+4,a4n+5中,a4n+3最大,令a4k+3=bk,由数列的恒等式和等比数列的求和公式,求出bn的通项,即可得到bn的范围,进而得到M的最小值.
解答 解:由题意可得数列{an}中的前几项:
1,3,5,$\frac{5}{2}$,$\frac{5}{4}$,$\frac{13}{4}$,$\frac{21}{4}$,$\frac{21}{8}$,$\frac{21}{16}$,$\frac{53}{16}$,$\frac{85}{16}$,$\frac{85}{32}$,$\frac{85}{64}$,$\frac{213}{64}$,$\frac{341}{64}$,…,
观察得到,连续5项,a4n+1,a4n+2,a4n+3,a4n+4,a4n+5中,a4n+3最大,
令a4k+3=bk,b0=5,b1=$\frac{21}{4}$,b2=$\frac{85}{16}$,b3=$\frac{341}{64}$,…,
若bk=$\frac{{x}_{k}}{{4}^{k}}$,则bk+1=$\frac{4{x}_{k}+1}{{4}^{k+1}}$=$\frac{{x}_{k}}{{4}^{k}}$+$\frac{1}{{4}^{k+1}}$=bk+$\frac{1}{{4}^{k+1}}$,
即有bk+1-bk=$\frac{1}{{4}^{k+1}}$,
则有bn=b0+(b1-b0)+…+(bn-bn-1)
=5+$\frac{1}{4}$+$\frac{1}{16}$+…$\frac{1}{{4}^{n}}$=5+$\frac{\frac{1}{4}(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}$=$\frac{16}{3}$-$\frac{1}{3•{4}^{n}}$,
即a4n+3=$\frac{16}{3}$-$\frac{1}{3•{4}^{n}}$是递增数列,
且a4n+3<$\frac{16}{3}$,
由于对每个n,a4n+1,a4n+2,a4n+3,a4n+4,a4n+5中,a4n+3最大,
则对n∈N,都有an<$\frac{16}{3}$.
由an<M恒成立,
则有M≥$\frac{16}{3}$.即M的最小值为$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 本题为2012年江西预赛试题的改编题,考查数列的通项及单调性和最值问题,同时考查等比数列的求和公式,以及化简运算能力,属于难题.

| A. | [-1,$\frac{7}{5}$] | B. | [0,$\frac{7}{4}$] | C. | [-2,$\frac{7}{3}$] | D. | [-2,$\frac{7}{5}$] |
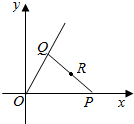 如图,已知P为x轴正半轴上的动点,Q为射线y=$\sqrt{3}$x(x>0)上的动点,△POQ的面积为8,求线段PQ的中心R的轨迹的参数方程.
如图,已知P为x轴正半轴上的动点,Q为射线y=$\sqrt{3}$x(x>0)上的动点,△POQ的面积为8,求线段PQ的中心R的轨迹的参数方程.