题目内容
10．直线y=2x-1关于直线y=$\frac{1}{2}$x-1对称的直线方程为2x+11y+11=0．分析 设所求直线上任意一点为P（x，y），则P关于直线y=$\frac{1}{2}$x-1的对称点P′（m，n）在直线y=2x-1上，由对称性可得mn的方程组，解得mn代入直线y=2x-1变形可得．
解答 解：设所求直线上任意一点为P（x，y），
则P关于直线y=$\frac{1}{2}$x-1的对称点P′（m，n）在直线y=2x-1上，
由对称性可得$\left\{\begin{array}{l}{\frac{y-n}{x-m}•\frac{1}{2}=-1}\\{\frac{y+n}{2}=\frac{1}{2}•\frac{m+x}{2}-1}\end{array}\right.$，解得$\left\{\begin{array}{l}{m=\frac{1}{5}（3x+4y+4）}\\{n=\frac{1}{5}（4x-3y-8）}\end{array}\right.$，
代入直线y=2x-1可得$\frac{1}{5}$（4x-3y-8）=$\frac{2}{5}$（3x+4y+4）-1，
化简可得所求直线方程为：2x+11y+11=0
故答案为：2x+11y+11=0
点评 本题考查直线的对称性，涉及直线的垂直关系和中点公式，属中档题．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
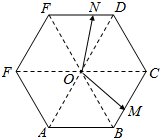如图，正六边形ABCDEF的边长为1，O为其中心，M，N分别是BC，DE上的动点，且|$\overrightarrow{BM}$|=|$\overrightarrow{DN}$|．