Question

【题目】如图，△OAB是等腰三角形，∠AOB=120°．以O为圆心， OA为半径作圆．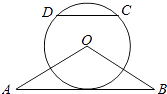

（1）证明：直线AB与⊙O相切；
（2）点C，D在⊙O上，且A，B，C，D四点共圆，证明：AB∥CD．

Answer 1

【答案】
（1）证明：设K为AB中点，连结OK，

∵OA=OB，∠AOB=120°，

∴OK⊥AB，∠A=30°，OK=OAsin30°= OA，

∴直线AB与⊙O相切；

（2）解：因为OA=2OD，所以O不是A，B，C，D四点所在圆的圆心．设T是A，B，C，D四点所在圆的圆心．

∵OA=OB，TA=TB，

∴OT为AB的中垂线，

同理，OC=OD，TC=TD，

∴OT为CD的中垂线，

∴AB∥CD

【解析】（1）设K为AB中点，连结OK．根据等腰三角形AOB的性质知OK⊥AB，∠A=30°，OK=OAsin30°= OA，则AB是圆O的切线．（2）设圆心为T，证明OT为AB的中垂线，OT为CD的中垂线，即可证明结论．