题目内容
【题目】已知函数f(x)=kx2+(3+k)x+3,其中k为常数,且k≠0.
(1)若f(2)=3,求函数f(x)的表达式;
(2)在(1)的条件下,设函数g(x)=f(x)﹣mx,若g(x)在区间[﹣2,2]上是单调函数,求实数m的取值范围;
(3)是否存在k使得函数f(x)在[﹣1,4]上的最大值是4?若存在,求出k的值;若不存在,请说明理由.
【答案】
(1)解:由f(2)=3,可得4k+2(3+k)+3=3,∴k=﹣1
∴f(x)=﹣x2+2x+3
(2)解:由(1)得g(x)=f(x)﹣mx=﹣x2+(2﹣m)x+3,函数的对称轴为x= ![]()
∵g(x)在区间[﹣2,2]上是单调函数,
∴ ![]() 或
或 ![]()
∴m≤﹣2或m≥6
(3)解:f(x)=kx2+(3+k)x+3的对称轴为 ![]()
①k>0时,函数图象开口向上, ![]() ,此时函数f(x)在[﹣1,4]上的最大值是f(4)=16k+(3+k)×4+3=20k+15=4,∴
,此时函数f(x)在[﹣1,4]上的最大值是f(4)=16k+(3+k)×4+3=20k+15=4,∴ ![]() ,不合题意,舍去;
,不合题意,舍去;
②k<0时,函数图象开口向下, ![]() ,
,
1°若 ![]() ,即
,即 ![]() 时,函数f(x)在[﹣1,4]上的最大值是f(
时,函数f(x)在[﹣1,4]上的最大值是f( ![]() )=
)= ![]()
∴k2+10k+9=0,∴k=﹣1或k=﹣9,符合题意;
2°若 ![]() ,即
,即 ![]() 时,函数f(x)在[﹣1,4]上递增,最大值为f(4)=16k+(3+k)×4+3=20k+15=4,
时,函数f(x)在[﹣1,4]上递增,最大值为f(4)=16k+(3+k)×4+3=20k+15=4,
∴ ![]() ,不合题意,舍去;
,不合题意,舍去;
综上,存在k使得函数f(x)在[﹣1,4]上的最大值是4,且k=﹣1或k=﹣9
【解析】(1)由f(2)=3,可得k的值,从而可得函数f(x)的表达式;(2)g(x)=f(x)﹣mx=﹣x2+(2﹣m)x+3,函数的对称轴为x= ![]() ,根据g(x)在区间[﹣2,2]上是单调函数,可得
,根据g(x)在区间[﹣2,2]上是单调函数,可得 ![]() 或
或 ![]() ,从而可求实数m的取值范围;(3)f(x)=kx2+(3+k)x+3的对称轴为
,从而可求实数m的取值范围;(3)f(x)=kx2+(3+k)x+3的对称轴为 ![]() ,分类讨论,确定函数图象开口向上,函数f(x)在[﹣1,4]上的单调性,利用最大值是4,建立方程,即可求得结论.
,分类讨论,确定函数图象开口向上,函数f(x)在[﹣1,4]上的单调性,利用最大值是4,建立方程,即可求得结论.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

【题目】已知某企业近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
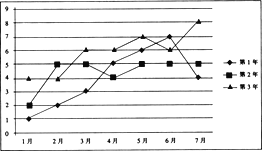
(1)试问这3年的前7个月中哪个月的月平均利润最高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
月份x | 1 | 2 | 3 | 4 |
利润y(单位:百万元) | 4 | 4 | 6 | 6 |
相关公式: 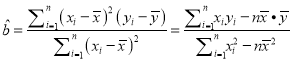 ,
, ![]() .
.
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班![]() 人进行了问卷调查得到了如下的列联表:已知在全部
人进行了问卷调查得到了如下的列联表:已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到喜爱打篮球的学生的概率为
人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整(不用写计算过程);并求出:有多大把握认为喜爱打篮球与性别有关,说明你的理由;
(2)若从该班不喜爱打篮球的男生中随机抽取3人调查,求其中某男生甲被选到的概率。下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
(参考公式:  ,其中
,其中![]() )
)