题目内容
【题目】已知椭圆C的中心在原点,焦点在![]() 轴上,离心率等于
轴上,离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点。
的焦点。
(1)求椭圆C的标准方程。
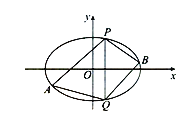
(2)已知点![]() 在椭圆C上,点A、B是椭圆C上不同于P、Q的两个动点,且满足:
在椭圆C上,点A、B是椭圆C上不同于P、Q的两个动点,且满足: ![]() 。试问:直线AB的斜率是否为定值?请说明理由。
。试问:直线AB的斜率是否为定值?请说明理由。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:对于(1),结合已知即可求出b2与a2,问题便可解答;
对于(2),当![]() 时,PA,PB的斜率之和为0.设直线PA的斜率为k,则PB的斜率为-k,接下来求出直线PA与PB的方程,然后将其与椭圆分别联立,即可求出
时,PA,PB的斜率之和为0.设直线PA的斜率为k,则PB的斜率为-k,接下来求出直线PA与PB的方程,然后将其与椭圆分别联立,即可求出![]() ,然后利用斜率的计算公式不难求出k的值,问题便可解答.
,然后利用斜率的计算公式不难求出k的值,问题便可解答.
试题解析:
(1)∵椭圆C的中心在原点,焦点在x轴上,∴设椭圆标准方程为![]() (a>b>0),
(a>b>0),
∵椭圆离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点.
的焦点.
![]() 焦点为(0,2
焦点为(0,2![]() ),
),
∴b=2![]() …(1分)e=
…(1分)e=![]() =
=![]() ,a2﹣b2=c2,
,a2﹣b2=c2,
∴解得a2=16,b2=12
∴椭圆C的标准方程![]() .
.
(2)直线 x=﹣2与椭圆![]() 交点P(﹣2,3),Q(﹣2,﹣3)或P(﹣2,﹣3),Q(﹣2,3),∴|PQ|=6,设A (x1,y1 ),B( x2,y2),
交点P(﹣2,3),Q(﹣2,﹣3)或P(﹣2,﹣3),Q(﹣2,3),∴|PQ|=6,设A (x1,y1 ),B( x2,y2),
当∠APQ=∠BPQ时直线PA,PB斜率之和为0.
设PA斜率为k,则PB斜率为﹣k.
当P(﹣2,3),Q(﹣2,﹣3)时,
PA的直线方程为y﹣3=k(x+2)
与椭圆联立得(3+4k2)x2+8k(2k+3)x+4(2k+3)2﹣48=0
∴![]() =
=![]() ;
;
同理 ![]()
∴ ![]()
![]() , y1﹣y2=k(x1+2)+3﹣[﹣k(x2+2)+3]=
, y1﹣y2=k(x1+2)+3﹣[﹣k(x2+2)+3]= ![]()
直线AB斜率为 ![]()

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】为了解患肺心病是否与性别有关,在某医院对入院者用简单随机抽样方法抽取50人进行调查,结果如下列联表:

(Ⅰ)是否有![]() 的把握认为入院者中患肺心病与性别有关?请说明理由;
的把握认为入院者中患肺心病与性别有关?请说明理由;
(Ⅱ)已知在患肺心病的10位女性中,有3位患胃病.现在从这10位女性中,随机选出3名进行其它方面的排查,记选出患胃病的女性人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 .
.