题目内容
5.已知函数f(x)=$\sqrt{3}$sin2x+2cos2x+a(1)求函数f(x)的最小正周期以及单调递增区间;
(2)当x∈[0,$\frac{π}{4}$]时,函数f(x)有最大值4,求实数a的取值范围.
分析 (1)由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性、单调性求得函数f(x)的最小正周期以及单调递增区间.
(2)由条件利用正弦函数的定义域和值域求得函数f(x)的最大值,再根据最大值为4求得a的值.
解答 解:(1)函数f(x)=$\sqrt{3}$sin2x+2cos2x+a=$\sqrt{3}$sin2x+cos2x+1+a=2sin(2x+$\frac{π}{6}$)+a+1,
故函数的周期为$\frac{2π}{2}$=π.
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈z,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,故函数的单调区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈z.
(2)当x∈[0,$\frac{π}{4}$]时,2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],函数f(x)的最大值为2+a+1=4,∴a=1.
点评 本题主要考查三角恒等变换,正弦函数的周期性、单调性、定义域和值域,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
14.已知函数f(x)=2sin(x+φ)(0<φ<π)是偶函数,则2cos(2φ+$\frac{π}{3}$)等于( )
| A. | -$\sqrt{3}$ | B. | -1 | C. | $\sqrt{3}$ | D. | 1 |
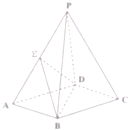 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC,求证:
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC,求证: