Question

【题目】某品牌经销商在一广场随机采访男性和女性用户各50名，其中每天玩微信超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如下：

	微信控	非微信控	合计
男性	26	24	50
女性	30	20	50
合计	56	44	100

（1）根据以上数据，能否有95%的把握认为“微信控”与“性别”有关？

（2）现从调查的女性用户中按分层抽样的方法选出5人，求所抽取的5人中“微信控”和“非微信控”的人数；

（3）从（2）中抽取的5位女性中，再随机抽取3人赠送礼品，试求抽取3人中恰有2人位“微信控”的概率.

参考公式: ，其中.

参考数据：

	0.50	0.40	0.25	0.15	0.10	0.05	0.025
	0.455	0.708	1.323	2.072	2.706	3.841	5.024

Answer 1

【答案】（1）没有的把握认为“微信控”与“性别”有关；（2）；（3）.

【解析】试题分析：（1）利用列联表，计算K2，对照数表得出概率结论；

（2）利用分层抽样原理计算从女性中选出5人时“微信控”与“非微信控”人数；

（3）利用列举法计算基本事件数，求出对应的概率值．

试题解析：

（1）由列联表可得

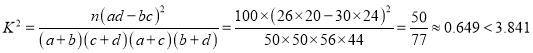
所以没有的把握认为“微信控”与“性别”有关．

（2）根据题意所抽取的位女性中，“微信控”有人，“非微信控”有人．

（3）抽取的位女性中，“微信控”人分别记为， ， ；“非微信控” 人分别记为， ．则再从中随机抽取人构成的所有基本事件为： ， ， ， ， ， ， ， ， ， ，共有种；抽取人中恰有人为“微信控”所含基本事件为： ， ， ， ， ， ，共有种，

所求为．