Question

【题目】（1）已知是奇函数，求常数m的值；

（2）画出函数的图象，并利用图象回答：k为何值时，方程 无解？有一解？有两解？

Answer 1

【答案】(1)见解析； （2）当k=0或k1时,方程有一解; 当0<k<1时,方程有两解。

【解析】

(1)先求出函数的定义域,再利用奇函数的定义,代入一对相反变量即可直接求常数m的值;

(2)先取绝对值画出分段函数图象,再利用函数的零点即为对应的两个函数图象的交点，把y=k在图象上进行上下平移由两个函数图象交点个数即可找到结论.

（1）

函数定义域是

又函数是奇函数，

，即

解得：m=1

（2）函数图像如图：

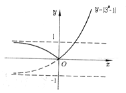
方程根的个数即为函数与函数y=k交点的个数，由（1）中函数图像可知：

当k<0时，直线y=k与函数的图象无交点,即方程无解;

当k=0或k1时, 直线y=k与函数的图象有唯一的交点，所以方程有一解;

当0<k<1时, 直线y=k与函数的图象有两个不同交点，所以方程有两解.

综上所述：k<0时，方程无解；k=0或k1方程有一解; 0<k<1方程有两解.