题目内容
设函数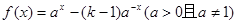 是定义域为
是定义域为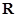 的奇函数.
的奇函数.
(Ⅰ)求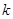 的值;
的值;
(Ⅱ)若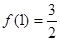 ,且
,且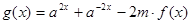 在
在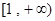 上的最小值为
上的最小值为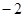 ,求
,求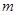 的值.
的值.
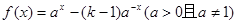 是定义域为
是定义域为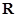 的奇函数.
的奇函数.(Ⅰ)求
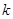 的值;
的值;(Ⅱ)若
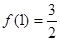 ,且
,且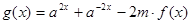 在
在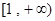 上的最小值为
上的最小值为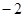 ,求
,求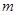 的值.
的值.(Ⅰ)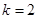 ; (Ⅱ)
; (Ⅱ)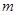 的值是
的值是 .
.
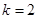 ; (Ⅱ)
; (Ⅱ)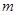 的值是
的值是 .
.试题分析:(Ⅰ)根据奇函数定义,对任意
 ,
,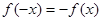 求
求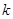 ;(Ⅱ)由(1)和条件
;(Ⅱ)由(1)和条件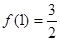 ,确定
,确定 ,然后令
,然后令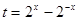 ,将
,将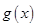 化为,
化为, ,
, ,将问题转化为在定区间上求二次函数最值.利用
,将问题转化为在定区间上求二次函数最值.利用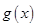 在
在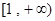 上的最小值为
上的最小值为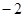 确定
确定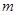 .试题解析:(1)由题意,对任意
.试题解析:(1)由题意,对任意 ,
,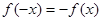 ,即
,即 ,
, 即
 ,
,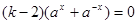 ,因为
,因为 为任意实数,
为任意实数,所以
 .
. (2)由(1)
 ,因为
,因为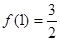 ,所以
,所以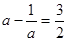 ,解得
,解得 .
. 故
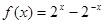 ,
,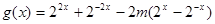 ,
,令
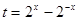 ,则
,则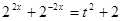 ,由
,由 ,得
,得 ,
,所以
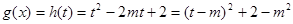 ,
,
当
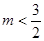 时,
时,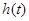 在
在 上是增函数,则
上是增函数,则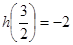 ,
, ,解得
,解得 (舍去).
(舍去). 当
 时,则
时,则 ,
, ,解得
,解得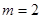 ,或
,或 (舍去).
(舍去).综上,
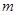 的值是
的值是 .
.
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 上的函数
上的函数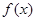 同时满足:①
同时满足:①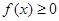 ;②
;②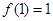 ;③若
;③若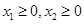 ,且
,且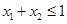 ,则
,则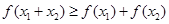 成立.则称函数
成立.则称函数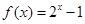 在区间
在区间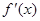 和
和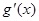 分别是
分别是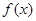 和
和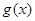 的导函数,若
的导函数,若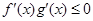 在区间
在区间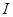 上恒成立,则称
上恒成立,则称 与
与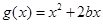 在开区间
在开区间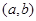 上单调性相反(
上单调性相反(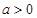 ),则
),则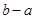 的最大值为 .
的最大值为 .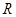 上的偶函数
上的偶函数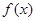 满足
满足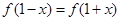 ,若
,若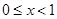 时,
时,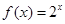 ,则
,则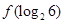 = .
= .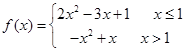 ,关于x的方程f(x)=m(m∈R)恰有三个互不相等的实数根
,关于x的方程f(x)=m(m∈R)恰有三个互不相等的实数根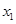 ,
,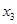 ,
,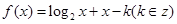 在区间(2,3)上有零点,则
在区间(2,3)上有零点,则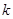 = .
= .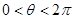 ,且方程
,且方程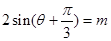 有两个不同的实数根,则这两个实根的和为 .
有两个不同的实数根,则这两个实根的和为 . 的图象恰好通过
的图象恰好通过 个格点,则称函数
个格点,则称函数 阶格点函数. 给出下列4个函数:
阶格点函数. 给出下列4个函数: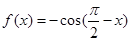 ;②
;②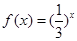 ;③
;③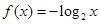 ;④
;④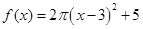 .
.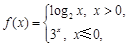 ,则
,则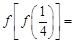 .
.