题目内容
11.把函数f(x)=sinx(x∈[0,2π])的图象向右平移$\frac{π}{3}$个单位后得到函数g(x)的图象,则f(x)与g(x)的图象所围成的面积为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 2 |
分析 根据三角函数的图象变换关系以及积分的应用即可得到结论.
解答 解:函数f(x)=sinx(x∈[0,2π])的图象向右平移$\frac{π}{3}$个单位后得到函数$g(x)=sin(x-\frac{π}{3})$,
令$sinx=sin(x-\frac{π}{3}),x∈[0,2π]$,
解得$x=\frac{2π}{3}$或$x=\frac{5π}{3}$,
故$S=\int_{\frac{2π}{3}}^{\frac{5π}{3}}{[sin(x-\frac{π}{3})-sinx]}dx=2$.
故选:D
点评 本题主要考查三角函数的图象变换关系以及利用积分求区域面积,考查学生的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的相关数据,如表所示.
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)求x,y的值.
(2)求顾客一次购物的结算时间超过2分钟的概率.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)求x,y的值.
(2)求顾客一次购物的结算时间超过2分钟的概率.
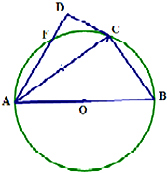 已知AB是⊙O的直径,F为圆上一点,∠BAF的角平分线与圆交于点C,过点C作圆的切线与直线AF相交于点D,若AB=6,∠DAB=$\frac{π}{3}$
已知AB是⊙O的直径,F为圆上一点,∠BAF的角平分线与圆交于点C,过点C作圆的切线与直线AF相交于点D,若AB=6,∠DAB=$\frac{π}{3}$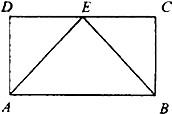 如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.
如图,在矩形ABCD中,点E为边CD上任意一点,现有质地均匀的粒子散落在矩形ABCD内,则粒子落在△ABE内的概率等于$\frac{1}{2}$.