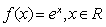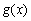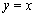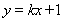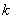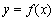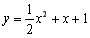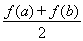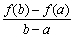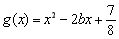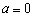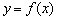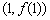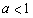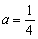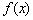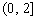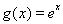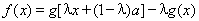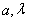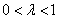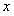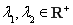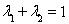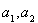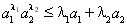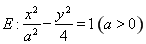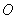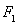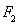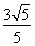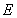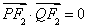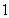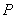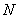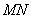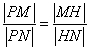题目内容
已知函数 ,
,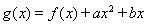 ,函数
,函数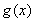 的图象在点
的图象在点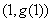 处的切线平行于
处的切线平行于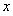 轴.
轴.
(1)确定 与
与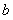 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意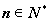 ,都有
,都有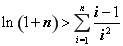 成立。
成立。
(1)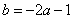 (2)当
(2)当 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在 单调递减;当
单调递减;当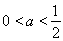 时,函数
时,函数 在
在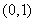 单调递增,在
单调递增,在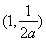 单调递减;在
单调递减;在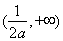 上单调递增;当
上单调递增;当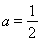 时,函数
时,函数 在
在 上单调递增,当
上单调递增,当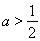 时,函数
时,函数 在
在 上单调递增,在
上单调递增,在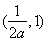 单调递减;在
单调递减;在 上单调递增(3)见解析
上单调递增(3)见解析
【解析】(1)依题意得 ,则
,则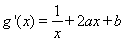
由函数 的图象在点
的图象在点 处的切线平行于
处的切线平行于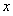 轴得:
轴得: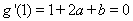
 ∴
∴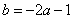 -------------------------------------3分
-------------------------------------3分
(2)由(1)得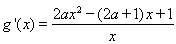
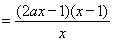 ----------4分
----------4分
∵函数 的定义域为
的定义域为
∴当 时,
时,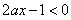 在
在 上恒成立,
上恒成立,
由 得
得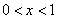 ,由
,由 得
得 ,
,
即函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在 单调递减;----------------5分
单调递减;----------------5分
当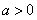 时,令
时,令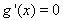 得
得 或
或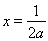 ,
,
若 ,即
,即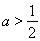 时,由
时,由 得
得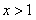 或
或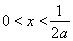 ,由
,由 得
得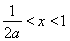 ,
,
即函数 在
在 ,
, 上单调递增,在
上单调递增,在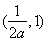 单调递减;---------6分
单调递减;---------6分
若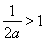 ,即
,即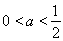 时,由
时,由 得
得 或
或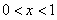 ,由
,由 得
得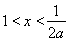 ,
,
即函数 在
在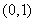 ,
,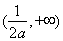 上单调递增,在
上单调递增,在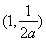 单调递减;------------7分
单调递减;------------7分
若 ,即
,即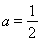 时,在
时,在 上恒有
上恒有 ,
,
即函数 在
在 上单调递增, -----------------8分
上单调递增, -----------------8分
综上得:当 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在 单调递减;
单调递减;
当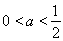 时,函数
时,函数 在
在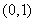 单调递增,在
单调递增,在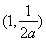 单调递减;在
单调递减;在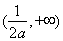 上单调递增;
上单调递增;
当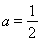 时,函数
时,函数 在
在 上单调递增,
上单调递增,
当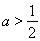 时,函数
时,函数 在
在 上单调递增,在
上单调递增,在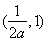 单调递减;在
单调递减;在 上单调递增.
上单调递增.
(3)证法一:由(2)知当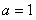 时,函数
时,函数 在
在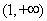 单调递增,
单调递增, ,即
,即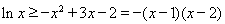 ,------------11分
,------------11分
令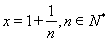 ,则
,则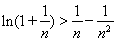 ,-------------------------------------12分
,-------------------------------------12分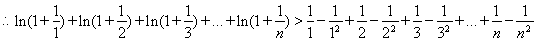
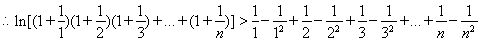
即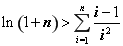 --------14分
--------14分
证法二:构造数列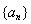 ,使其前
,使其前 项和
项和 ,
,
则当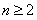 时,
时,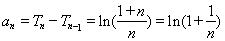 ,-------11分
,-------11分
显然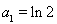 也满足该式,
也满足该式,
故只需证 -------------------12分
-------------------12分
令 ,即证
,即证 ,记
,记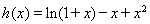 ,
,
则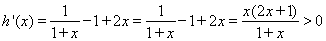 ,
,
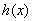 在
在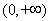 上单调递增,故
上单调递增,故 ,
,
∴ 成立,
成立,
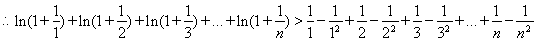
即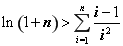 . -14分
. -14分

练习册系列答案
相关题目