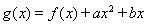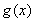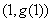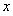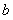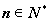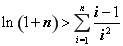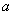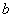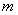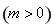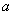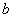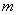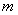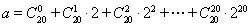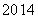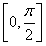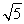题目内容
过椭圆Γ: =1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
=1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为 .
.
(1)求椭圆Γ的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆Γ恒有两个交点P,Q,且 ⊥
⊥ ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
(1) +y2=1(2)存在圆心在原点的圆x2+y2=
+y2=1(2)存在圆心在原点的圆x2+y2=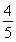 满足条件
满足条件
【解析】(1)由已知得 解得
解得 ∴b2=a2-c2=1,
∴b2=a2-c2=1,
故椭圆Γ的方程为 +y2=1.
+y2=1.
(2)假设满足条件的圆存在,其方程为x2+y2=r2(0<r<1).
当直线PQ的斜率存在时,设其方程为y=kx+t,
由 消去y整理得(1+4k2)x2+8ktx+4t2-4=0.
消去y整理得(1+4k2)x2+8ktx+4t2-4=0.
设P(x1,y1),Q(x2,y2),
则x1+x2=- ,x1x2=
,x1x2=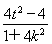 .①
.①
∵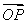 ⊥
⊥ ,∴x1x2+y1y2=0.
,∴x1x2+y1y2=0.
又y1=kx1+t,y2=kx2+t,
∴x1x2+(kx1+t)(kx2+t)=0,
即(1+k2)x1x2+kt(x1+x2)+t2=0.②
将①代入②得 +t2=0,?
+t2=0,?
即t2= (1+k2).
(1+k2).
∵直线PQ与圆x2+y2=r2相切,
∴r= ∈(0,1),
∈(0,1),
∴存在圆x2+y2= 满足条件.
满足条件.
当直线PQ的斜率不存在时,也适合x2+y2=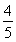 .
.
综上所述,存在圆心在原点的圆x2+y2=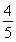 满足条件.
满足条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目