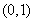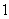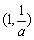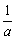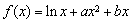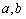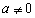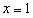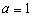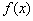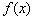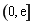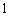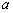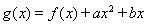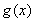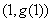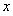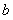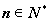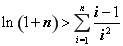题目内容
已知函数 ,
, 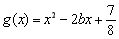 .
.
(Ⅰ)当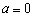 时,求曲线
时,求曲线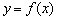 在点
在点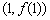 处的切线方程;
处的切线方程;
(Ⅱ)当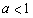 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当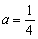 时,函数
时,函数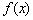 在
在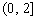 上的最大值为
上的最大值为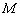 ,若存在
,若存在 ,使得
,使得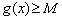 成立,求实数b的取值范围.
成立,求实数b的取值范围.
(Ⅰ)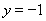 (Ⅱ)当
(Ⅱ)当 时,递增区间为
时,递增区间为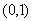 ,
,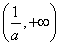 ,递减区间为
,递减区间为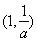
当 时,函数
时,函数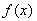 的递增区间为
的递增区间为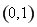 ,递减区间为
,递减区间为
【解析】(Ⅰ)当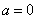 时,
时,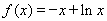
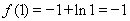 ……………………1分
……………………1分
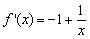
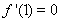 …………………………………….…2分
…………………………………….…2分
所以曲线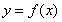 在点
在点 处的切线方程
处的切线方程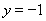 …………………………….…3分
…………………………….…3分
(Ⅱ)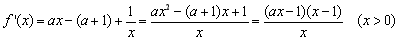 ………4分
………4分
当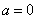 时,
时,
解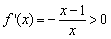 ,得
,得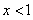 ,解
,解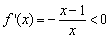 ,得
,得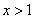
所以函数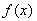 的递增区间为
的递增区间为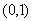 ,递减区间为在
,递减区间为在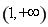 ………………………5分
………………………5分
x | |
|
|
|
| |||||
f’(x) | + |
| - |
| + | |||||
f(x) | 增 |
| 减 |
| 增 | |||||
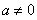 时,令
时,令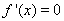 得
得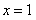 或
或
当 时,
时,
函数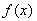 的递增区间为
的递增区间为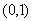 ,
,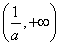 ,递减区间为
,递减区间为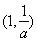 ……………………7分
……………………7分
当 时,
时,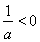 在
在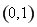 上
上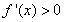 ,在
,在 上
上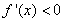 8分
8分
函数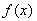 的递增区间为
的递增区间为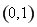 ,递减区间为
,递减区间为 ………………………9分
………………………9分
(Ⅲ)由(Ⅱ)知,当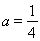 时,
时, 在
在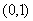 上是增函数,在
上是增函数,在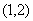 上是减函数,
上是减函数,
所以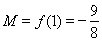 , ……………………………11分
, ……………………………11分
存在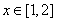 ,使
,使 即存在
即存在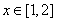 ,使
,使 ,
,
方法一:只需函数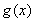 在[1,2]上的最大值大于等于
在[1,2]上的最大值大于等于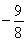
所以有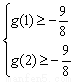 即
即 解得:
解得: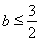 …13分
…13分
方法二:将
整理得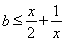
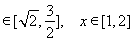 从而有
从而有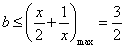
所以 的取值范围是
的取值范围是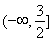 .………13分
.………13分

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目